Question Number 66171 by mathmax by abdo last updated on 10/Aug/19
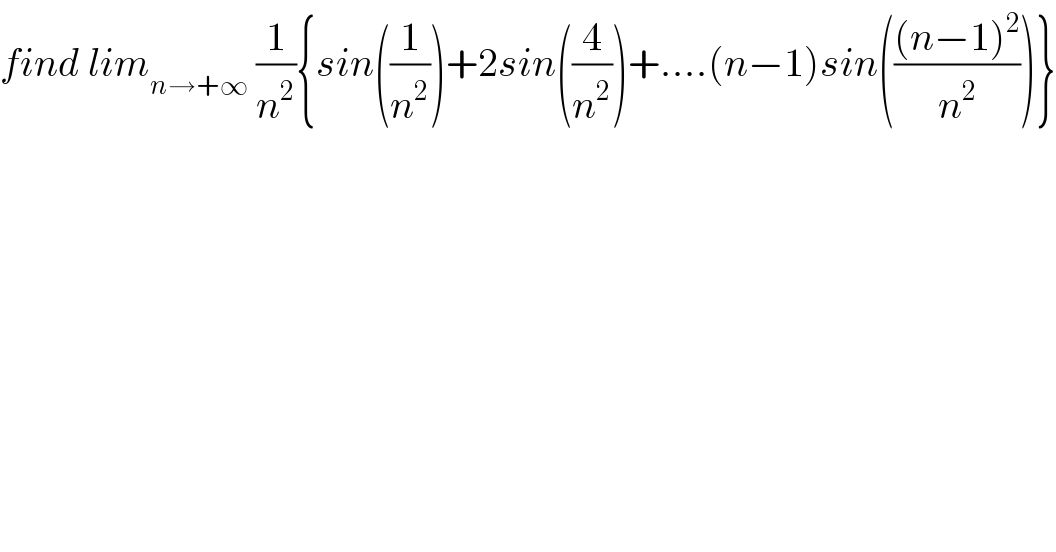
$${find}\:{lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left\{{sin}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)+\mathrm{2}{sin}\left(\frac{\mathrm{4}}{{n}^{\mathrm{2}} }\right)+….\left({n}−\mathrm{1}\right){sin}\left(\frac{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\right\} \\ $$
Commented by mathmax by abdo last updated on 10/Aug/19
![let S_n =(1/n^2 ){sin((1/n^2 ))+2sin((4/n^2 ))+...+(n−1)sin((((n−1)^2 )/n^2 ))} we have S_n =(1/n^2 )Σ_(k=0) ^(n−1) k sin((k^2 /n^2 )) =(1/n)Σ_(k=0) ^(n−1) ((k/n))sin((k^2 /n^2 )) S_n is a Rieman sum ⇒lim_(n→+∞) S_n =∫_0 ^1 xsin(x^2 )dx =[−(1/2)cos(x^2 )]_0 ^1 =−(1/2)(cos(1)−1)=(1/2) −((cos(1))/2).](https://www.tinkutara.com/question/Q66188.png)
$${let}\:{S}_{{n}} =\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left\{{sin}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)+\mathrm{2}{sin}\left(\frac{\mathrm{4}}{{n}^{\mathrm{2}} }\right)+…+\left({n}−\mathrm{1}\right){sin}\left(\frac{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\right\} \\ $$$${we}\:{have}\:{S}_{{n}} =\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k}\:{sin}\left(\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\:=\frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left(\frac{{k}}{{n}}\right){sin}\left(\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$${S}_{{n}} {is}\:{a}\:{Rieman}\:{sum}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} {xsin}\left({x}^{\mathrm{2}} \right){dx} \\ $$$$=\left[−\frac{\mathrm{1}}{\mathrm{2}}{cos}\left({x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=−\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\left(\mathrm{1}\right)−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{{cos}\left(\mathrm{1}\right)}{\mathrm{2}}. \\ $$
Answered by Smail last updated on 10/Aug/19
![lim_(n→∞) (1/n^2 )(sin(1/n^2 )+2sin(4/n^2 )+...+(n−1)sin((((n−1)^2 )/n^2 ))) lim_(n→∞) (1/n)×(1/n)(sin(1/n^2 )+2sin(4/n^2 )+...+(n−1)sin((((n−1)^2 )/n^2 ))) lim_(n→∞) (1/n)((1/n)sin(1/n^2 )+(2/n)sin(4/n^2 )+...+((n−1)/n)sin((((n−1)^2 )/n^2 ))) =lim_(n→∞) ((1−0)/n)Σ_(k=1) ^(n−1) (k/n)sin(((k/n))^2 ) =∫_0 ^1 xsin(x^2 )dx−lim_(n→∞) (1/n)((n/n)sin(((n/n))^2 )) =−(1/2)[cos(x^2 )]_0 ^1 =(1/2)(1−cos(1)) =sin^2 ((1/2))](https://www.tinkutara.com/question/Q66176.png)
$$\underset{{n}\rightarrow\infty} {{lim}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left({sin}\left(\mathrm{1}/{n}^{\mathrm{2}} \right)+\mathrm{2}{sin}\left(\mathrm{4}/{n}^{\mathrm{2}} \right)+…+\left({n}−\mathrm{1}\right){sin}\left(\frac{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\right) \\ $$$$\underset{{n}\rightarrow\infty} {{lim}}\frac{\mathrm{1}}{{n}}×\frac{\mathrm{1}}{{n}}\left({sin}\left(\mathrm{1}/{n}^{\mathrm{2}} \right)+\mathrm{2}{sin}\left(\mathrm{4}/{n}^{\mathrm{2}} \right)+…+\left({n}−\mathrm{1}\right){sin}\left(\frac{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\right) \\ $$$$\underset{{n}\rightarrow\infty} {{lim}}\frac{\mathrm{1}}{{n}}\left(\frac{\mathrm{1}}{{n}}{sin}\left(\mathrm{1}/{n}^{\mathrm{2}} \right)+\frac{\mathrm{2}}{{n}}{sin}\left(\mathrm{4}/{n}^{\mathrm{2}} \right)+…+\frac{{n}−\mathrm{1}}{{n}}{sin}\left(\frac{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\right) \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\frac{\mathrm{1}−\mathrm{0}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{{k}}{{n}}{sin}\left(\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} \right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {xsin}\left({x}^{\mathrm{2}} \right){dx}−\underset{{n}\rightarrow\infty} {{lim}}\frac{\mathrm{1}}{{n}}\left(\frac{{n}}{{n}}{sin}\left(\left(\frac{{n}}{{n}}\right)^{\mathrm{2}} \right)\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left[{cos}\left({x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{cos}\left(\mathrm{1}\right)\right) \\ $$$$={sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
