Question Number 66341 by mathmax by abdo last updated on 12/Aug/19
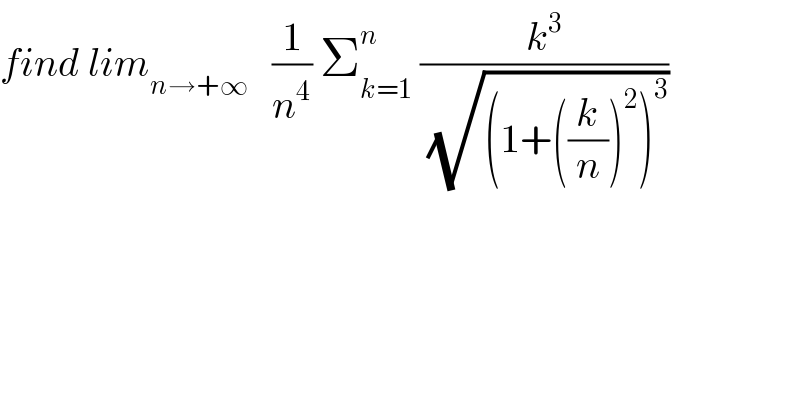
$${find}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\frac{\mathrm{1}}{{n}^{\mathrm{4}} }\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}^{\mathrm{3}} }{\:\sqrt{\left(\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} \right)^{\mathrm{3}} }} \\ $$
Commented by Prithwish sen last updated on 13/Aug/19
![(1/n)lim_(n→∞) Σ_(k=1) ^n ((((k/n))^3 )/( (√((1+((k/n))^2 )^3 )))) = ∫_0 ^1 (x^3 /( (√((1+x^2 )^3 )))) dx =[((2+x^2 )/( (√(1+x^2 ))))]_0 ^1 =((3−2(√2))/( (√2)))](https://www.tinkutara.com/question/Q66360.png)
$$\frac{\mathrm{1}}{\mathrm{n}}\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{3}} }{\:\sqrt{\left(\mathrm{1}+\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} \right)^{\mathrm{3}} }}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{3}} }{\:\sqrt{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}\:\mathrm{dx} \\ $$$$=\left[\frac{\mathrm{2}+\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}} \\ $$
