Question Number 78263 by msup trace by abdo last updated on 15/Jan/20
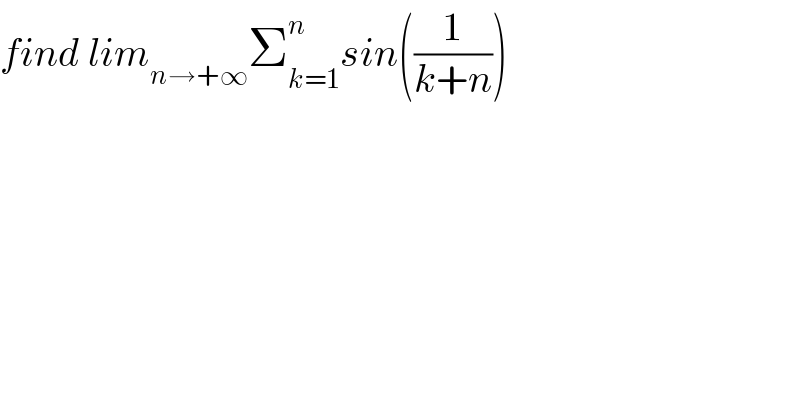
$${find}\:{lim}_{{n}\rightarrow+\infty} \sum_{{k}=\mathrm{1}} ^{{n}} {sin}\left(\frac{\mathrm{1}}{{k}+{n}}\right) \\ $$
Commented by jagoll last updated on 15/Jan/20

$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{{k}+{n}}\right)=\mathrm{0} \\ $$
Commented by msup trace by abdo last updated on 15/Jan/20

$${show}\:{your}\:{work}\:{sir}.{its}\:{insufficient}… \\ $$
Answered by mind is power last updated on 15/Jan/20
![lemna ∀x>0 x−(x^3 /6)≤sin(x)≤x proff since sin(x)=Σ_(k≥0) (((−1)^k x^(2k+1) )/((2k+1)!))=x−(x^3 /6)+Σ_(k≥2) (((−1)^k x^(2k+1) )/((2k+1)!))≥x−(x^3 /6) sin(x)=x+Σ_(k≥1) (((−1)^k x^(2k+1) )/((2k+1)!))<x ⇒ x−(x^3 /6)<sin(x)<x ∀k∈[1,n] ∀n∈N^∗ we have (1/(k+n))−(1/6)((1/(k+n)))^3 <sin((1/(k+n)))<(1/(k+n)) ⇒Σ_(k=1) ^n {((1/(k+n)))−(1/(6(k+n)^3 ))}<Σ_(k=1) ^n sin((1/(k+n)))<Σ_(k=1) ^n (1/(k+n)) lim_(n→∞) Σ_(k=1) ^n (1/(n+k))=lim_(n→∞) (1/n)Σ_(k=1) ^n (1/(1+(k/n)))=∫_0 ^1 (dx/(1+x))=ln(2) Σ_(k=1) ^n (1/((n+k)^3 ))≤(1/n^2 ).Σ_(k=1) ^n (1/(n+k))≤((ln(2))/n^2 )→0 lim_(n→∞) {Σ_(k=1) ^n (1/(k+n))−(1/6)Σ_(k=1) ^n (1/((n+k)^3 ))}<lim_(n→∞) Σsin((1/(k+n)))<lim_(n→∞) Σ(1/(n+k)) ln(2)≤lim_(n→∞) Σ_(k=1) ^n sin((1/(n+k)))≤ln(2) lim_(n→∞) Σsin((1/(n+k)))=ln(2)](https://www.tinkutara.com/question/Q78294.png)
$$\:\:\:\mathrm{lemna} \\ $$$$\forall\mathrm{x}>\mathrm{0} \\ $$$$\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\leqslant\mathrm{sin}\left(\mathrm{x}\right)\leqslant\mathrm{x} \\ $$$$\mathrm{proff} \\ $$$$\mathrm{since} \\ $$$$\mathrm{sin}\left(\mathrm{x}\right)=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{x}^{\mathrm{2k}+\mathrm{1}} }{\left(\mathrm{2k}+\mathrm{1}\right)!}=\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}+\underset{\mathrm{k}\geqslant\mathrm{2}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{x}^{\mathrm{2k}+\mathrm{1}} }{\left(\mathrm{2k}+\mathrm{1}\right)!}\geqslant\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}} \\ $$$$\mathrm{sin}\left(\mathrm{x}\right)=\mathrm{x}+\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{x}^{\mathrm{2k}+\mathrm{1}} }{\left(\mathrm{2k}+\mathrm{1}\right)!}<\mathrm{x} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}<\mathrm{sin}\left(\mathrm{x}\right)<\mathrm{x} \\ $$$$\forall\mathrm{k}\in\left[\mathrm{1},\mathrm{n}\right]\:\forall\mathrm{n}\in\mathbb{N}^{\ast} \:\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{1}}{\mathrm{k}+\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{1}}{\mathrm{k}+\mathrm{n}}\right)^{\mathrm{3}} <\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{k}+\mathrm{n}}\right)<\frac{\mathrm{1}}{\mathrm{k}+\mathrm{n}} \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left\{\left(\frac{\mathrm{1}}{\mathrm{k}+\mathrm{n}}\right)−\frac{\mathrm{1}}{\mathrm{6}\left(\mathrm{k}+\mathrm{n}\right)^{\mathrm{3}} }\right\}<\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{k}+\mathrm{n}}\right)<\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}+\mathrm{n}} \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}}=\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{k}\right)^{\mathrm{3}} }\leqslant\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }.\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}\leqslant\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{n}^{\mathrm{2}} }\rightarrow\mathrm{0} \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left\{\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}+\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{6}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{k}\right)^{\mathrm{3}} }\right\}<\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\Sigma\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{k}+\mathrm{n}}\right)<\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\Sigma\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}} \\ $$$$\mathrm{ln}\left(\mathrm{2}\right)\leqslant\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}\right)\leqslant\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\Sigma\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{k}}\right)=\mathrm{ln}\left(\mathrm{2}\right) \\ $$
Commented by msup trace by abdo last updated on 15/Jan/20

$${thank}\:{you}\:{sir}. \\ $$
Commented by mind is power last updated on 15/Jan/20

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$
