Question Number 8633 by Yozzias last updated on 19/Oct/16
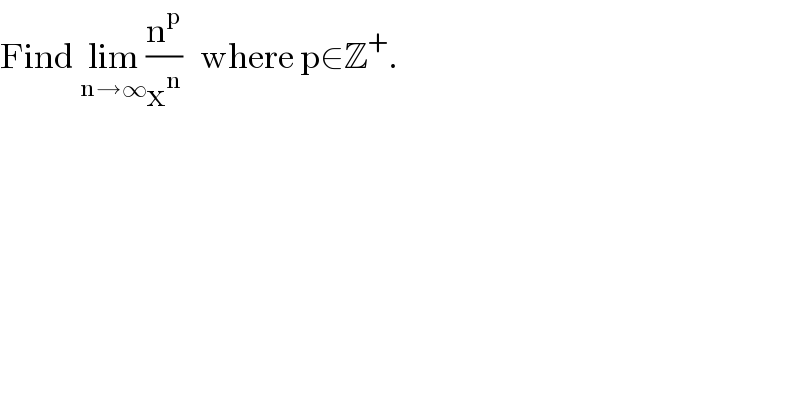
$$\mathrm{Find}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{n}^{\mathrm{p}} }{\mathrm{x}^{\mathrm{n}} }\:\:\:\mathrm{where}\:\mathrm{p}\in\mathbb{Z}^{+} . \\ $$
Commented by prakash jain last updated on 19/Oct/16
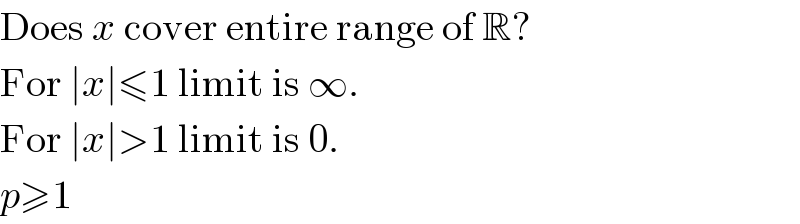
$$\mathrm{Does}\:{x}\:\mathrm{cover}\:\mathrm{entire}\:\mathrm{range}\:\mathrm{of}\:\mathbb{R}? \\ $$$$\mathrm{For}\:\mid{x}\mid\leqslant\mathrm{1}\:\mathrm{limit}\:\mathrm{is}\:\infty. \\ $$$$\mathrm{For}\:\mid{x}\mid>\mathrm{1}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{0}. \\ $$$${p}\geqslant\mathrm{1} \\ $$
Commented by Yozzias last updated on 19/Oct/16
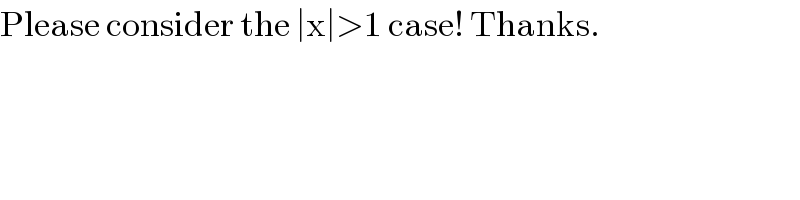
$$\mathrm{Please}\:\mathrm{consider}\:\mathrm{the}\:\mid\mathrm{x}\mid>\mathrm{1}\:\mathrm{case}!\:\mathrm{Thanks}. \\ $$
Answered by prakash jain last updated on 19/Oct/16
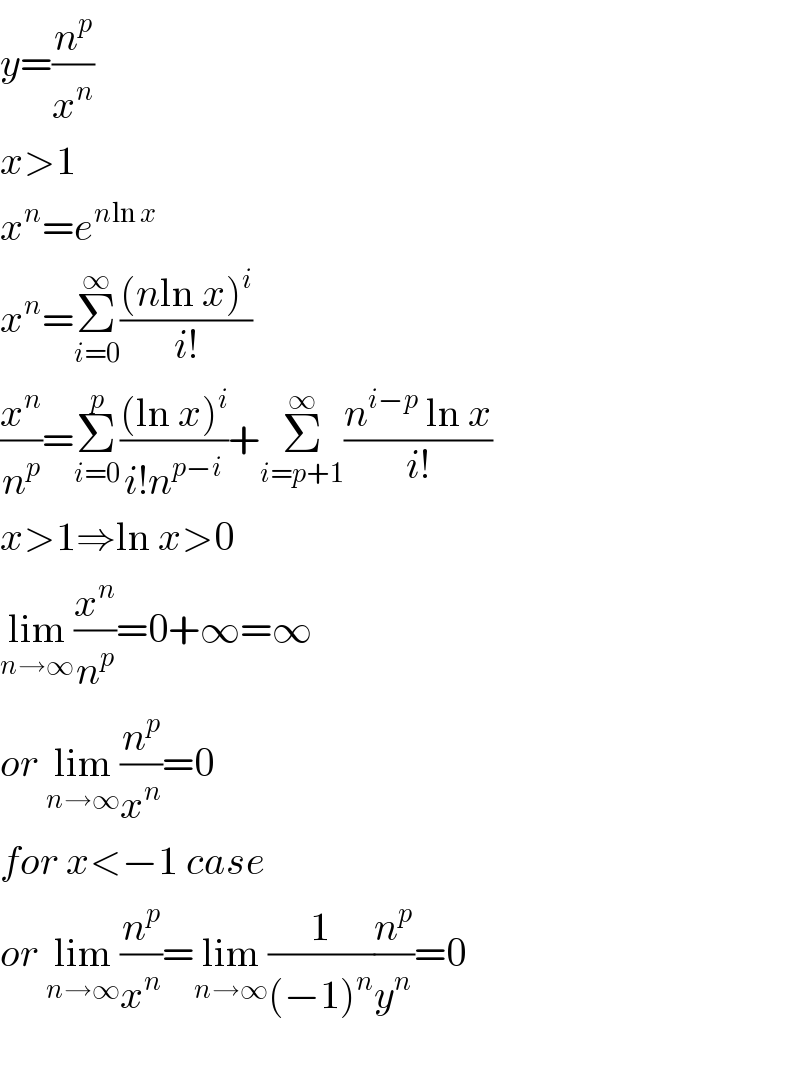
$${y}=\frac{{n}^{{p}} }{{x}^{{n}} } \\ $$$${x}>\mathrm{1} \\ $$$${x}^{{n}} ={e}^{{n}\mathrm{ln}\:{x}} \\ $$$${x}^{{n}} =\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left({n}\mathrm{ln}\:{x}\right)^{{i}} }{{i}!} \\ $$$$\frac{{x}^{{n}} }{{n}^{{p}} }=\underset{{i}=\mathrm{0}} {\overset{{p}} {\sum}}\frac{\left(\mathrm{ln}\:{x}\right)^{{i}} }{{i}!{n}^{{p}−{i}} }+\underset{{i}={p}+\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{{i}−{p}} \:\mathrm{ln}\:{x}}{{i}!} \\ $$$${x}>\mathrm{1}\Rightarrow\mathrm{ln}\:{x}>\mathrm{0} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{{n}} }{{n}^{{p}} }=\mathrm{0}+\infty=\infty \\ $$$${or}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{p}} }{{x}^{{n}} }=\mathrm{0} \\ $$$${for}\:{x}<−\mathrm{1}\:{case} \\ $$$${or}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{p}} }{{x}^{{n}} }=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\left(−\mathrm{1}\right)^{{n}} }\frac{{n}^{{p}} }{{y}^{{n}} }=\mathrm{0} \\ $$$$ \\ $$
