Question Number 133830 by metamorfose last updated on 24/Feb/21
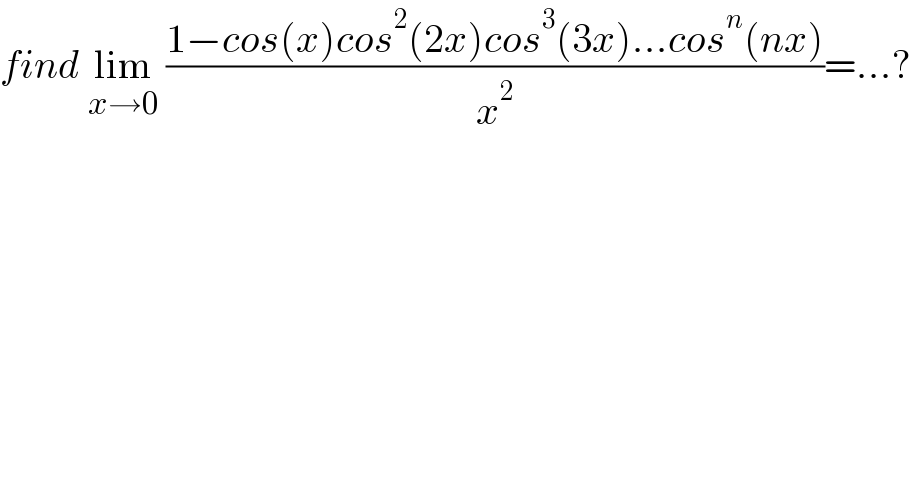
$${find}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−{cos}\left({x}\right){cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right){cos}^{\mathrm{3}} \left(\mathrm{3}{x}\right)…{cos}^{{n}} \left({nx}\right)}{{x}^{\mathrm{2}} }=…? \\ $$
Answered by EDWIN88 last updated on 24/Feb/21
![lim_(x→0) ((1−(1−(1/2)x^2 )(1−(8/2)x^2 )(1−((27)/2)x^2 )...(1−(n^3 /2)x^2 ))/x^2 )= lim_(x→0) ((1−(1−(1/2)x^2 (1^3 +2^3 +3^3 +...+n^3 )))/x^2 ) = (1/2)(1^3 +2^3 +3^3 +...+n^3 ) = (1/2) [((n(n+1))/2) ]^2](https://www.tinkutara.com/question/Q133831.png)
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{\mathrm{8}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\frac{\mathrm{27}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)…\left(\mathrm{1}−\frac{\mathrm{n}^{\mathrm{3}} }{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} }= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} +…+\mathrm{n}^{\mathrm{3}} \right)\right)}{\mathrm{x}^{\mathrm{2}} }\:= \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}^{\mathrm{3}} +\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{3}} +…+\mathrm{n}^{\mathrm{3}} \right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left[\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}\:\right]^{\mathrm{2}} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 24/Feb/21

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−{cos}\left({x}\right){cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right){cos}^{\mathrm{3}} \left(\mathrm{3}{x}\right)…{cos}^{{n}} \left({nx}\right)}{{x}^{\mathrm{2}} }={y} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{nlog}\left({cos}\left({nx}\right)\right)={log}\left(\mathrm{1}−{x}^{\mathrm{2}} {y}\right)\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:{log}\left(\mathrm{1}+{x}\right)={x} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{nlog}\left(\mathrm{1}−\frac{{n}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}}\right)={log}\left(\mathrm{1}−{x}^{\mathrm{2}} {y}\right)\:\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{cosx}=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$−\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{n}^{\mathrm{3}} {x}^{\mathrm{2}} }{\mathrm{2}}=−{x}^{\mathrm{2}} {y}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{n}^{\mathrm{3}} ={y} \\ $$$${y}=\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{8}} \\ $$
Answered by bramlexs22 last updated on 24/Feb/21

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x}}{\mathrm{x}^{\mathrm{2}} }\:=\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{x}\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{4x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} }\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{9}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$ \\ $$
