Question Number 73330 by mathmax by abdo last updated on 10/Nov/19
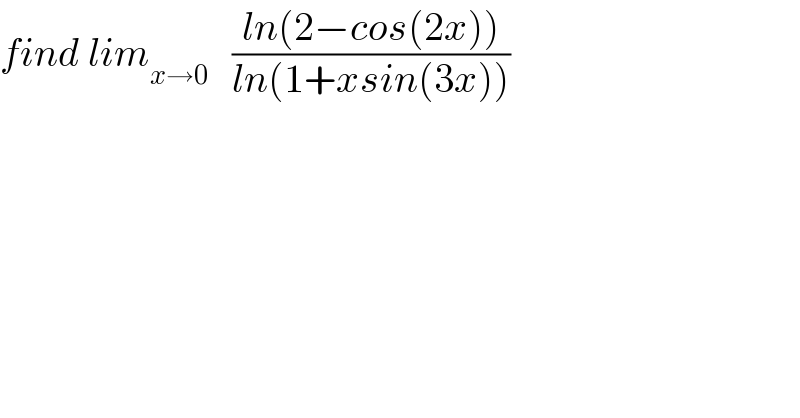
$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{ln}\left(\mathrm{2}−{cos}\left(\mathrm{2}{x}\right)\right)}{{ln}\left(\mathrm{1}+{xsin}\left(\mathrm{3}{x}\right)\right)} \\ $$
Commented by mathmax by abdo last updated on 11/Nov/19
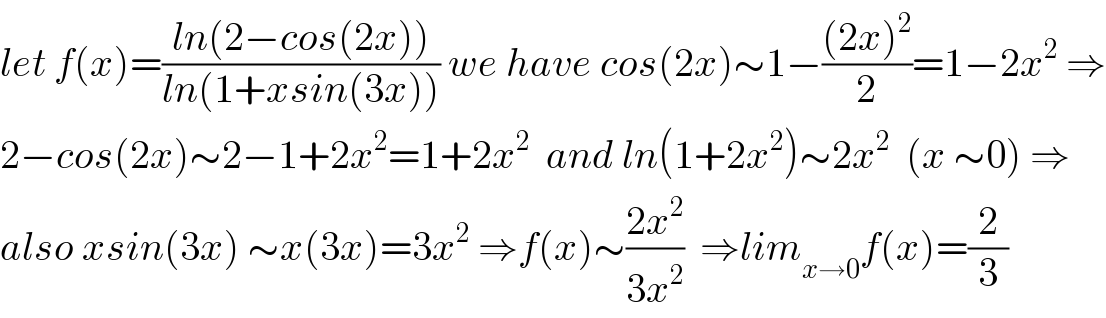
$${let}\:{f}\left({x}\right)=\frac{{ln}\left(\mathrm{2}−{cos}\left(\mathrm{2}{x}\right)\right)}{{ln}\left(\mathrm{1}+{xsin}\left(\mathrm{3}{x}\right)\right)}\:{we}\:{have}\:{cos}\left(\mathrm{2}{x}\right)\sim\mathrm{1}−\frac{\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{2}}=\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{2}−{cos}\left(\mathrm{2}{x}\right)\sim\mathrm{2}−\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} =\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} \:\:{and}\:{ln}\left(\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} \right)\sim\mathrm{2}{x}^{\mathrm{2}} \:\:\left({x}\:\sim\mathrm{0}\right)\:\Rightarrow \\ $$$${also}\:{xsin}\left(\mathrm{3}{x}\right)\:\sim{x}\left(\mathrm{3}{x}\right)=\mathrm{3}{x}^{\mathrm{2}} \:\Rightarrow{f}\left({x}\right)\sim\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{3}{x}^{\mathrm{2}} }\:\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Answered by Smail last updated on 10/Nov/19
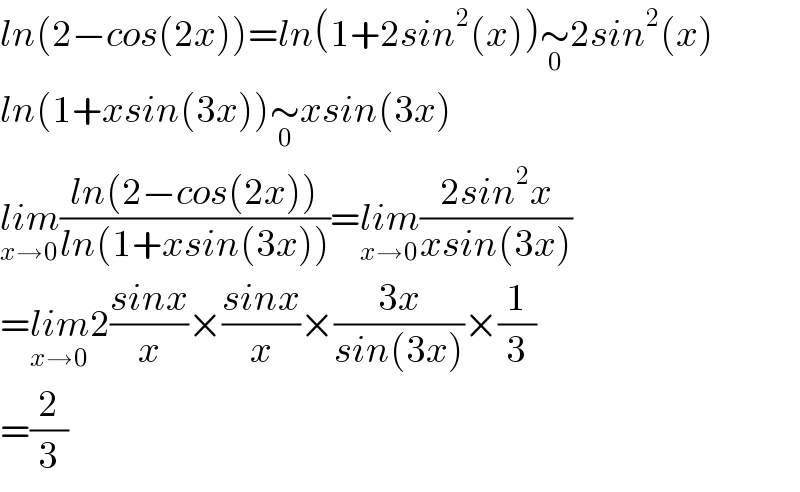
$${ln}\left(\mathrm{2}−{cos}\left(\mathrm{2}{x}\right)\right)={ln}\left(\mathrm{1}+\mathrm{2}{sin}^{\mathrm{2}} \left({x}\right)\right)\underset{\mathrm{0}} {\sim}\mathrm{2}{sin}^{\mathrm{2}} \left({x}\right) \\ $$$${ln}\left(\mathrm{1}+{xsin}\left(\mathrm{3}{x}\right)\right)\underset{\mathrm{0}} {\sim}{xsin}\left(\mathrm{3}{x}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{ln}\left(\mathrm{2}−{cos}\left(\mathrm{2}{x}\right)\right)}{{ln}\left(\mathrm{1}+{xsin}\left(\mathrm{3}{x}\right)\right)}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\mathrm{2}{sin}^{\mathrm{2}} {x}}{{xsin}\left(\mathrm{3}{x}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\mathrm{2}\frac{{sinx}}{{x}}×\frac{{sinx}}{{x}}×\frac{\mathrm{3}{x}}{{sin}\left(\mathrm{3}{x}\right)}×\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
