Menu Close

find-lim-x-0-sin-sin-1-cosx-1-cos-x-sinx-x-3-

Tinku Tara 0 Comments
Pin




Question Number 143730 by mathmax by abdo last updated on 17/Jun/21
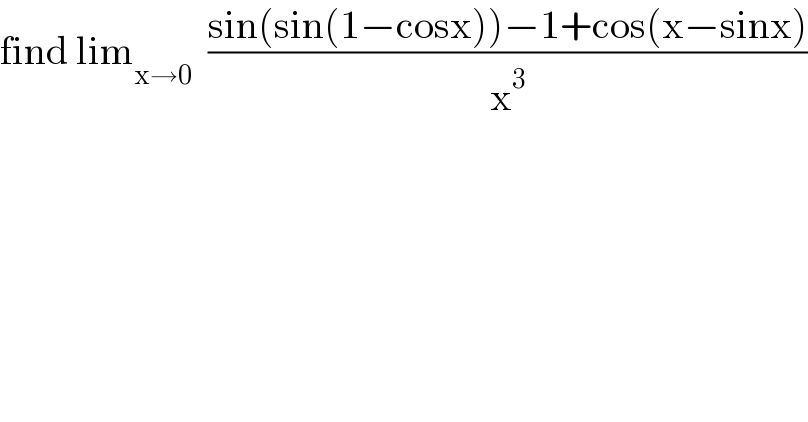
find lim_(x→0) ((sin(sin(1−cosx))−1+cos(x−sinx))/x^3 )
$$\mathrm{find}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{sin}\left(\mathrm{sin}\left(\mathrm{1}−\mathrm{cosx}\right)\right)−\mathrm{1}+\mathrm{cos}\left(\mathrm{x}−\mathrm{sinx}\right)}{\mathrm{x}^{\mathrm{3}} } \\ $$
Answered by TheHoneyCat last updated on 17/Jun/21
sinx=x−(x^3 /6)+o(x^4 ) x−sinx=(x^3 /6)+o(x^4 ) cosx=1−(x^2 /2)+o(x^3 ) thus: cosx=1+o(x^(12) ) so: −1+cosx=o(x^(12) )=o(x^3 ) 1−cosx=(x^2 /2)+o(x^3 ) so: sin(1−cosx)=(x^2 /2)+o(x^3 ) and thus: sin(sin(1−cosx))=(x^2 /2)+o(x^3 ) so in the end: ((sin(sin(1−cosx))−1+cos(x−sinx))/x^3 )=(1/(2x))+o(1) lim_(x→0^+ ) ((sin(sin(1−cosx))−1+cos(x−sinx))/x^3 )=+∞ lim_(x→0^− ) ((sin(sin(1−cosx))−1+cos(x−sinx))/x^3 )=−∞ so technicaly there is no such limit... but, we all get it I hope... ;•)
$$\mathrm{sin}{x}={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{o}\left({x}^{\mathrm{4}} \right) \\ $$$${x}−\mathrm{sin}{x}=\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{o}\left({x}^{\mathrm{4}} \right) \\ $$$$\mathrm{cos}{x}=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{3}} \right) \\ $$$$\mathrm{thus}:\:\mathrm{cos}{x}=\mathrm{1}+{o}\left({x}^{\mathrm{12}} \right) \\ $$$$\mathrm{so}:\:−\mathrm{1}+\mathrm{cos}{x}={o}\left({x}^{\mathrm{12}} \right)={o}\left({x}^{\mathrm{3}} \right) \\ $$$$ \\ $$$$\mathrm{1}−\mathrm{cos}{x}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{3}} \right) \\ $$$$\mathrm{so}:\:\mathrm{sin}\left(\mathrm{1}−\mathrm{cos}{x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{3}} \right) \\ $$$$\mathrm{and}\:\mathrm{thus}:\:\mathrm{sin}\left(\mathrm{sin}\left(\mathrm{1}−\mathrm{cos}{x}\right)\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{3}} \right) \\ $$$$ \\ $$$$\mathrm{so}\:\mathrm{in}\:\mathrm{the}\:\mathrm{end}: \\ $$$$\frac{\mathrm{sin}\left(\mathrm{sin}\left(\mathrm{1}−\mathrm{cosx}\right)\right)−\mathrm{1}+\mathrm{cos}\left(\mathrm{x}−\mathrm{sinx}\right)}{\mathrm{x}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{2}{x}}+{o}\left(\mathrm{1}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\frac{\mathrm{sin}\left(\mathrm{sin}\left(\mathrm{1}−\mathrm{cosx}\right)\right)−\mathrm{1}+\mathrm{cos}\left(\mathrm{x}−\mathrm{sinx}\right)}{\mathrm{x}^{\mathrm{3}} }=+\infty \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{−} } \:\:\frac{\mathrm{sin}\left(\mathrm{sin}\left(\mathrm{1}−\mathrm{cosx}\right)\right)−\mathrm{1}+\mathrm{cos}\left(\mathrm{x}−\mathrm{sinx}\right)}{\mathrm{x}^{\mathrm{3}} }=−\infty \\ $$$$ \\ $$$${so}\:{technicaly}\:{there}\:{is}\:{no}\:{such}\:{limit}… \\ $$$${but},\:{we}\:{all}\:{get}\:{it}\:{I}\:{hope}… \\ $$$$\left.;\bullet\right) \\ $$
Answered by mathmax by abdo last updated on 20/Jun/21
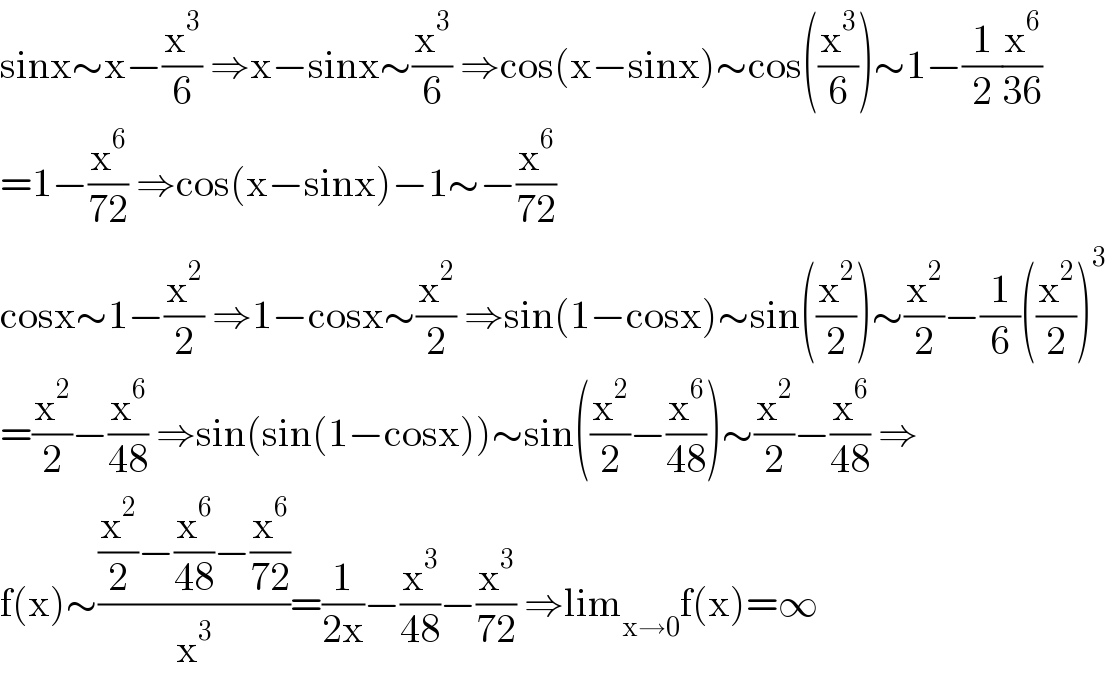
sinx∼x−(x^3 /6) ⇒x−sinx∼(x^3 /6) ⇒cos(x−sinx)∼cos((x^3 /6))∼1−(1/2)(x^6 /(36)) =1−(x^6 /(72)) ⇒cos(x−sinx)−1∼−(x^6 /(72)) cosx∼1−(x^2 /2) ⇒1−cosx∼(x^2 /2) ⇒sin(1−cosx)∼sin((x^2 /2))∼(x^2 /2)−(1/6)((x^2 /2))^3 =(x^2 /2)−(x^6 /(48)) ⇒sin(sin(1−cosx))∼sin((x^2 /2)−(x^6 /(48)))∼(x^2 /2)−(x^6 /(48)) ⇒ f(x)∼(((x^2 /2)−(x^6 /(48))−(x^6 /(72)))/x^3 )=(1/(2x))−(x^3 /(48))−(x^3 /(72)) ⇒lim_(x→0) f(x)=∞
$$\mathrm{sinx}\sim\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\:\Rightarrow\mathrm{x}−\mathrm{sinx}\sim\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\:\Rightarrow\mathrm{cos}\left(\mathrm{x}−\mathrm{sinx}\right)\sim\mathrm{cos}\left(\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)\sim\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{36}} \\ $$$$=\mathrm{1}−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{72}}\:\Rightarrow\mathrm{cos}\left(\mathrm{x}−\mathrm{sinx}\right)−\mathrm{1}\sim−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{72}} \\ $$$$\mathrm{cosx}\sim\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{1}−\mathrm{cosx}\sim\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{sin}\left(\mathrm{1}−\mathrm{cosx}\right)\sim\mathrm{sin}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sim\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{48}}\:\Rightarrow\mathrm{sin}\left(\mathrm{sin}\left(\mathrm{1}−\mathrm{cosx}\right)\right)\sim\mathrm{sin}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{48}}\right)\sim\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{48}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{48}}−\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{72}}}{\mathrm{x}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{2x}}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{48}}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{72}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)=\infty \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *