Question Number 74536 by mhmd last updated on 25/Nov/19
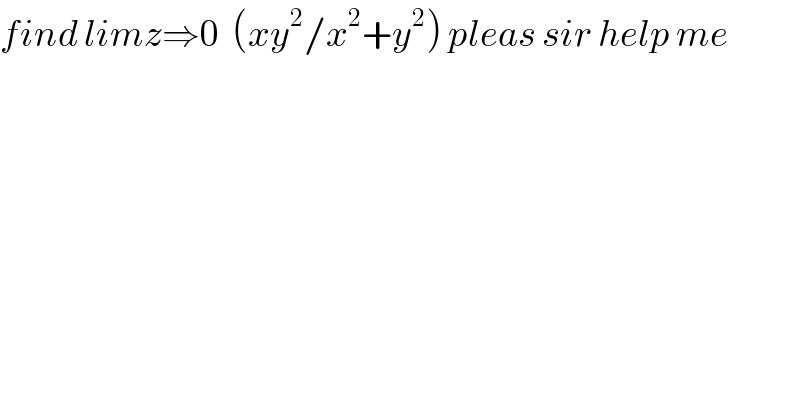
$${find}\:{limz}\Rightarrow\mathrm{0}\:\:\left({xy}^{\mathrm{2}} /{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\:{pleas}\:{sir}\:{help}\:{me}\: \\ $$
Answered by mind is power last updated on 26/Nov/19

$$\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\frac{{xy}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${f}\left({x},{y}\right)=\frac{{xy}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\frac{{xy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }.{y} \\ $$$$\forall\left({x},{y}\right)\in\mathbb{R}^{\ast^{\mathrm{2}} } \:\:\:\:\:{xy}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\frac{\mid{xy}\mid}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mid\frac{{xy}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\mid\leqslant\frac{\mid{y}\mid}{\mathrm{2}} \\ $$$$\underset{\left({x},{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} {\mathrm{lim}}\:{f}\left({x},{y}\right)=\mathrm{0} \\ $$
