Question Number 132531 by bemath last updated on 15/Feb/21
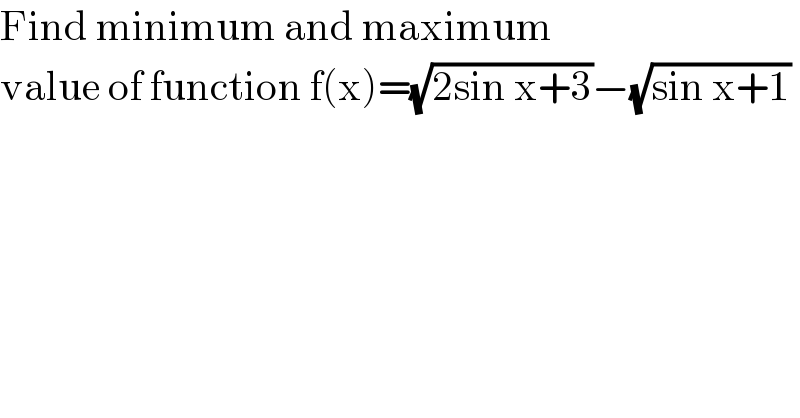
$$\mathrm{Find}\:\mathrm{minimum}\:\mathrm{and}\:\mathrm{maximum} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{function}\:\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\mathrm{2sin}\:\mathrm{x}+\mathrm{3}}−\sqrt{\mathrm{sin}\:\mathrm{x}+\mathrm{1}} \\ $$
Answered by liberty last updated on 15/Feb/21
![((df(x))/dx)=((cos x)/( (√(2sin x+3))))−((cos x)/(2(√(sin x+1)))) =0 ((cos x)/( (√(2sin x+3)))) = ((cos x)/(2(√(sin x+1)))) cos^2 x(4sin x+4)=cos^2 x(2sin x+3) cos^2 (x) [ 2sin x+1 ]=0 { ((cos^2 x=0 → { ((x=(π/2))),((x=((3π)/2))) :})),((sin x=−(1/2)→x=((7π)/6))) :} (1)f((π/2))=(√(2sin (π/2)+3))−(√(sin (π/2)+1)) = (√5)−(√2) ≈ 0.8219 (2)f(((3π)/2))= (√(2sin ((3π)/2)+3))−(√(sin ((3π)/2)+1)) = (√1) −(√0) = 1 (maximum) (3) f(((7π)/6))=(√(2sin ((7π)/6)+3))−(√(sin ((7π)/6)+1)) = (√2) −(1/( (√2))) = (1/( (√2))) ≈ 0.7071 (minimum)](https://www.tinkutara.com/question/Q132532.png)
$$\frac{\mathrm{df}\left(\mathrm{x}\right)}{\mathrm{dx}}=\frac{\mathrm{cos}\:\mathrm{x}}{\:\sqrt{\mathrm{2sin}\:\mathrm{x}+\mathrm{3}}}−\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{2}\sqrt{\mathrm{sin}\:\mathrm{x}+\mathrm{1}}}\:=\mathrm{0} \\ $$$$\:\frac{\mathrm{cos}\:\mathrm{x}}{\:\sqrt{\mathrm{2sin}\:\mathrm{x}+\mathrm{3}}}\:=\:\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{2}\sqrt{\mathrm{sin}\:\mathrm{x}+\mathrm{1}}} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\left(\mathrm{4sin}\:\mathrm{x}+\mathrm{4}\right)=\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\left(\mathrm{2sin}\:\mathrm{x}+\mathrm{3}\right) \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{x}\right)\:\left[\:\mathrm{2sin}\:\mathrm{x}+\mathrm{1}\:\right]=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}=\mathrm{0}\:\rightarrow\begin{cases}{\mathrm{x}=\frac{\pi}{\mathrm{2}}}\\{\mathrm{x}=\frac{\mathrm{3}\pi}{\mathrm{2}}}\end{cases}}\\{\mathrm{sin}\:\mathrm{x}=−\frac{\mathrm{1}}{\mathrm{2}}\rightarrow\mathrm{x}=\frac{\mathrm{7}\pi}{\mathrm{6}}}\end{cases} \\ $$$$\left(\mathrm{1}\right)\mathrm{f}\left(\frac{\pi}{\mathrm{2}}\right)=\sqrt{\mathrm{2sin}\:\frac{\pi}{\mathrm{2}}+\mathrm{3}}−\sqrt{\mathrm{sin}\:\frac{\pi}{\mathrm{2}}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\sqrt{\mathrm{5}}−\sqrt{\mathrm{2}}\:\approx\:\mathrm{0}.\mathrm{8219} \\ $$$$\left(\mathrm{2}\right)\mathrm{f}\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)=\:\sqrt{\mathrm{2sin}\:\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{3}}−\sqrt{\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{1}} \\ $$$$=\:\sqrt{\mathrm{1}}\:−\sqrt{\mathrm{0}}\:=\:\mathrm{1}\:\left(\mathrm{maximum}\right) \\ $$$$\left(\mathrm{3}\right)\:\mathrm{f}\left(\frac{\mathrm{7}\pi}{\mathrm{6}}\right)=\sqrt{\mathrm{2sin}\:\frac{\mathrm{7}\pi}{\mathrm{6}}+\mathrm{3}}−\sqrt{\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{6}}+\mathrm{1}} \\ $$$$\:=\:\sqrt{\mathrm{2}}\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\approx\:\mathrm{0}.\mathrm{7071}\:\left(\mathrm{minimum}\right) \\ $$
Commented by liberty last updated on 15/Feb/21

Answered by MJS_new last updated on 15/Feb/21
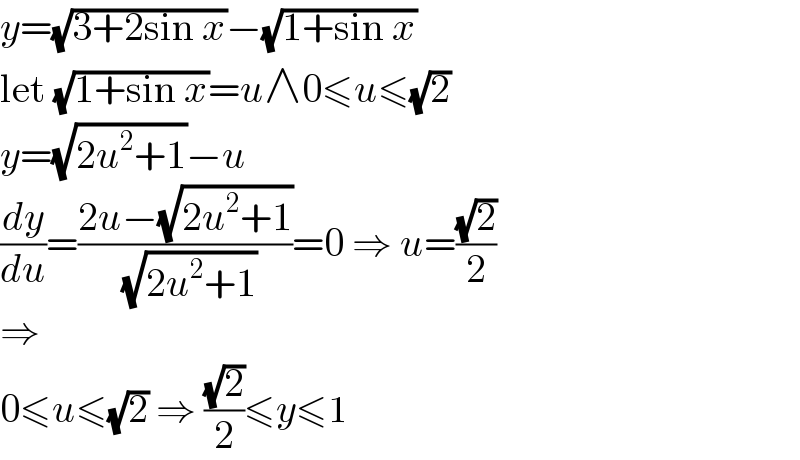
$${y}=\sqrt{\mathrm{3}+\mathrm{2sin}\:{x}}−\sqrt{\mathrm{1}+\mathrm{sin}\:{x}} \\ $$$$\mathrm{let}\:\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}={u}\wedge\mathrm{0}\leqslant{u}\leqslant\sqrt{\mathrm{2}} \\ $$$${y}=\sqrt{\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}}−{u} \\ $$$$\frac{{dy}}{{du}}=\frac{\mathrm{2}{u}−\sqrt{\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}}}=\mathrm{0}\:\Rightarrow\:{u}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\mathrm{0}\leqslant{u}\leqslant\sqrt{\mathrm{2}}\:\Rightarrow\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\leqslant{y}\leqslant\mathrm{1} \\ $$
