Question Number 67384 by mathmax by abdo last updated on 26/Aug/19
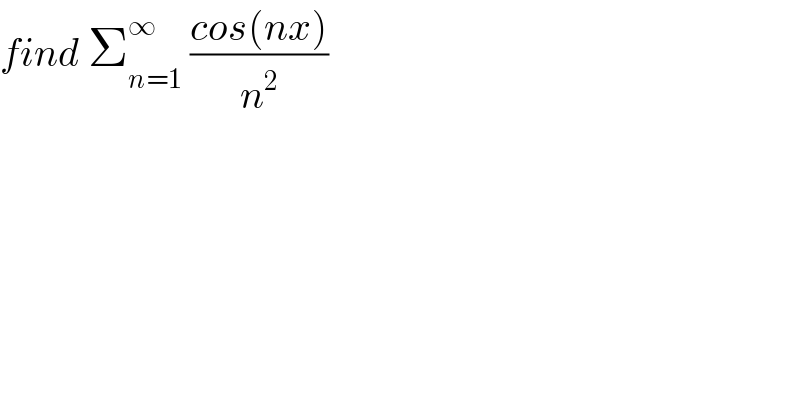
$${find}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{n}^{\mathrm{2}} } \\ $$
Commented by mathmax by abdo last updated on 27/Aug/19
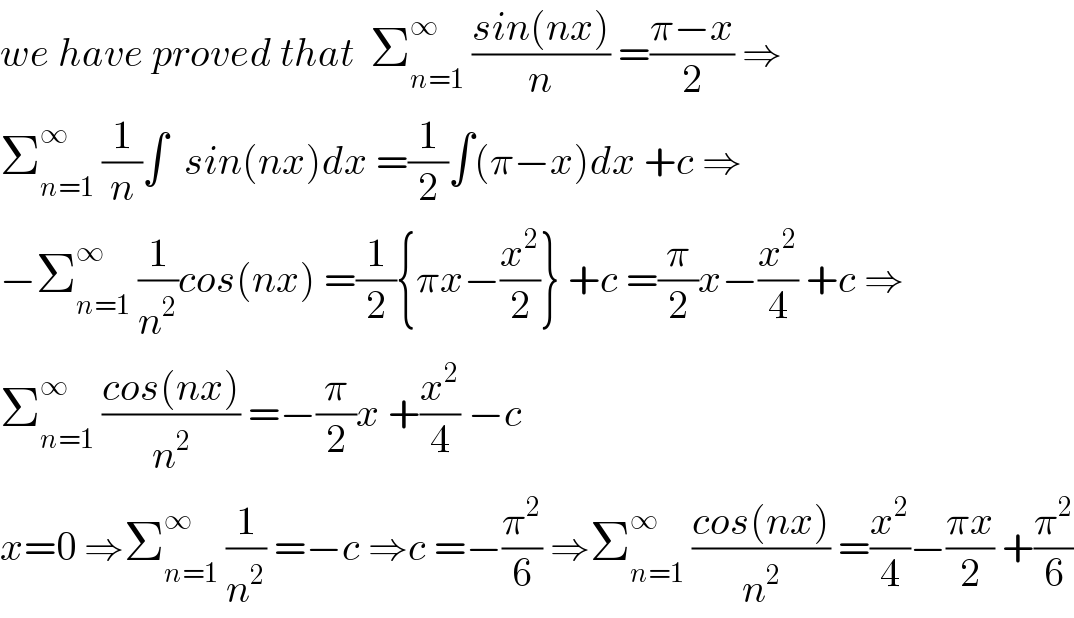
$${we}\:{have}\:{proved}\:{that}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({nx}\right)}{{n}}\:=\frac{\pi−{x}}{\mathrm{2}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\int\:\:{sin}\left({nx}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\pi−{x}\right){dx}\:+{c}\:\Rightarrow \\ $$$$−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }{cos}\left({nx}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\pi{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right\}\:+{c}\:=\frac{\pi}{\mathrm{2}}{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:+{c}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{n}^{\mathrm{2}} }\:=−\frac{\pi}{\mathrm{2}}{x}\:+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:−{c} \\ $$$${x}=\mathrm{0}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=−{c}\:\Rightarrow{c}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{n}^{\mathrm{2}} }\:=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}−\frac{\pi{x}}{\mathrm{2}}\:+\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
