Find-orthogonal-trajectories-of-the-curves-x-c-2-y-2-c-2-

Question Number 74040 by Learner-123 last updated on 18/Nov/19

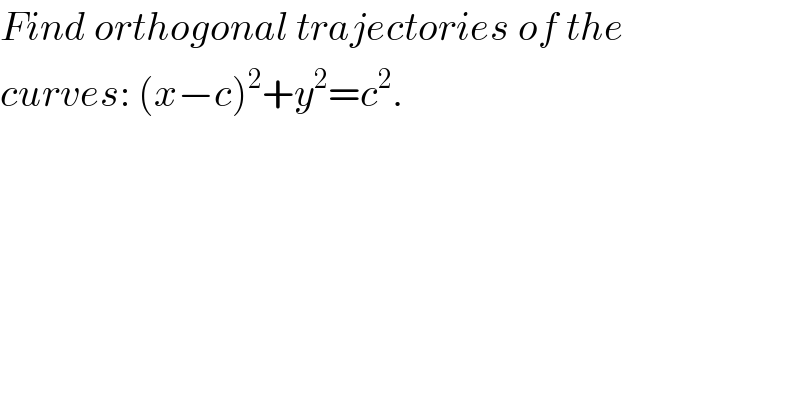
F i n d o r t h o g o n a l t r a j e c t o r i e s o f t h e

c u r v e s : {(x - c)}^{2} + y^{2} = c^{2} .

Commented by Learner-123 last updated on 18/Nov/19

p l e a s e h e l p \dots

Answered by mind is power last updated on 18/Nov/19

\Leftrightarrow x^{2} - 2 c x + y^{2} = 0

Γ_{c} b e e t h i s f a m i l y o f c u r v e s

\Rightarrow \frac{\partial}{\partial x} (x^{2} - 2 c x + y^{2}) = 0 = 2 x - 2 c + 2 \frac{d y}{d x} y = 0

\Rightarrow x - c + \frac{d y}{d x} . y = 0 \dots E

\frac{d y}{d x} i s d i r e c t i o n c o e f i c e n t o f t a n g e n t i n M (x, y)

i n o r t h o g o n a l t r a j e c t o r i e s

t a n g e n t w i l l b e e o r t o g o n a l

Γ_{c}^{'} i r t h o g o n a l t r a j e c t o r i e s o f Γ_{c}

M (x, S) \in Γ^{'} \Rightarrow t a n g e n t i s M h a s e d i r e c t o r c o e f i c i e n t

\frac{d Y}{d x} . \frac{d y}{d x} = - 1 \Rightarrow \frac{d y}{d x} = \frac{- d x}{d Y}

\Leftrightarrow E x - c - \frac{d x}{d Y} . Y = 0 \Leftrightarrow \frac{d Y}{Y} = \frac{d x}{x - c} \Rightarrow l n ∣ Y ∣= k (x - c)

\Rightarrow Y = k (x - c) l i g n

Commented by Learner-123 last updated on 19/Nov/19

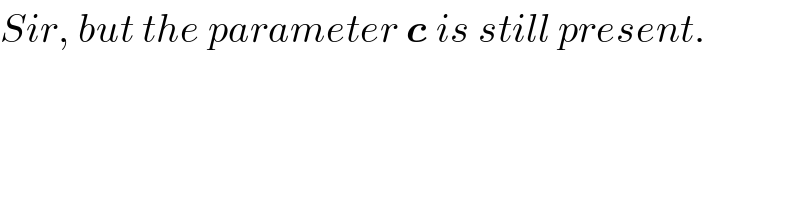
S i r, b u t t h e p a r a m e t e r c i s s t i l l p r e s e n t .

Commented by mind is power last updated on 19/Nov/19

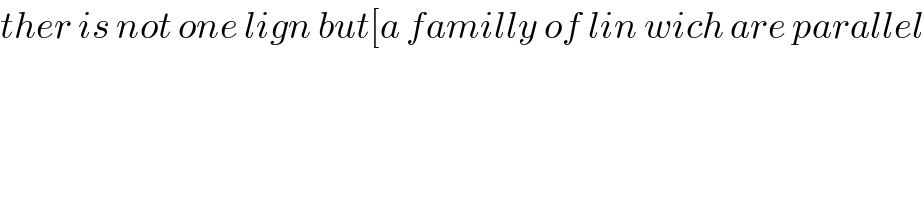
t h e r i s n o t o n e l i g n b u t [a f a m i l l y o f l i n w i c h a r e p a r a l l e l

Commented by Learner-123 last updated on 19/Nov/19

t h a n k s s i r .