Question Number 75080 by ~blr237~ last updated on 07/Dec/19
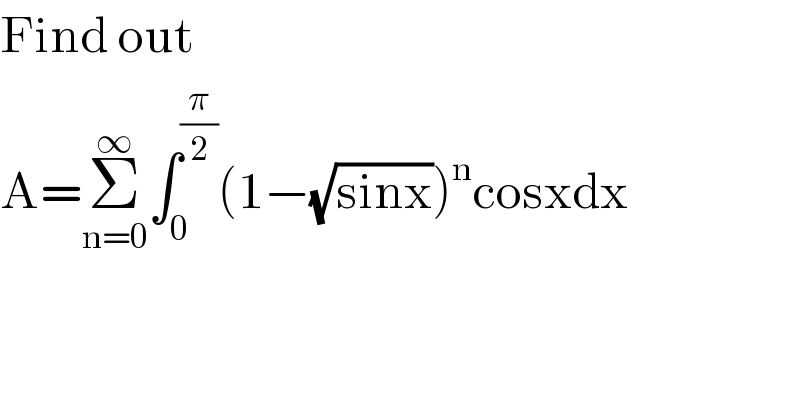
$$\mathrm{Find}\:\mathrm{out}\: \\ $$$$\mathrm{A}=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\sqrt{\mathrm{sinx}}\right)^{\mathrm{n}} \mathrm{cosxdx} \\ $$
Commented by mathmax by abdo last updated on 07/Dec/19
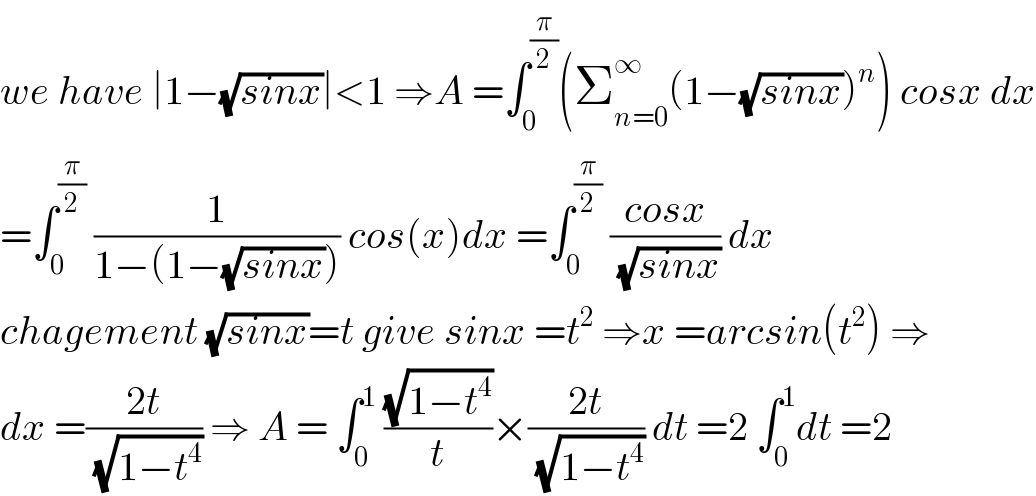
$${we}\:{have}\:\mid\mathrm{1}−\sqrt{{sinx}}\mid<\mathrm{1}\:\Rightarrow{A}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(\mathrm{1}−\sqrt{{sinx}}\right)^{{n}} \right)\:{cosx}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}}{\mathrm{1}−\left(\mathrm{1}−\sqrt{{sinx}}\right)}\:{cos}\left({x}\right){dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{cosx}}{\:\sqrt{{sinx}}}\:{dx} \\ $$$${chagement}\:\sqrt{{sinx}}={t}\:{give}\:{sinx}\:={t}^{\mathrm{2}} \:\Rightarrow{x}\:={arcsin}\left({t}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${dx}\:=\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}\:\Rightarrow\:{A}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}{{t}}×\frac{\mathrm{2}{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{4}} }}\:{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} {dt}\:=\mathrm{2} \\ $$
