Question Number 78490 by ~blr237~ last updated on 18/Jan/20
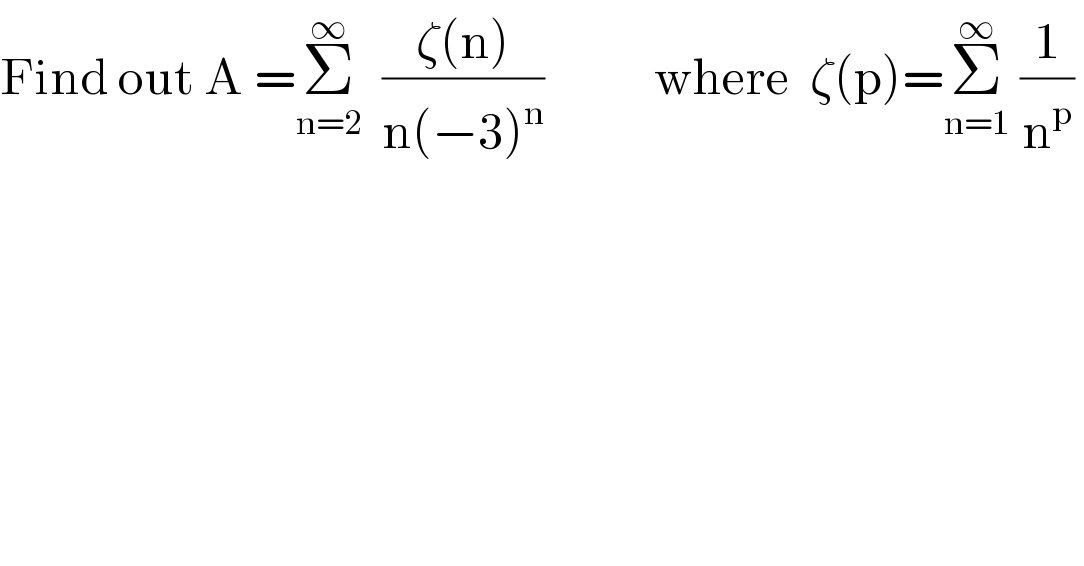
$$\mathrm{Find}\:\mathrm{out}\:\mathrm{A}\:=\underset{\mathrm{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\:\frac{\zeta\left(\mathrm{n}\right)}{\mathrm{n}\left(−\mathrm{3}\right)^{\mathrm{n}} }\:\:\:\:\:\:\:\:\:\:\:\mathrm{where}\:\:\zeta\left(\mathrm{p}\right)=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{p}} }\: \\ $$
Answered by mind is power last updated on 19/Jan/20
![let f(x)=Σ_(n≥2) ((ζ(n)x^n )/n)=Σ_(n≥2) (x^n /n)Σ_(m≥1) (1/m^n ) =Σ_(n≥2) .Σ_(m≥1) ((x/m))^n .(1/n) ∀n,m ,n≥2 and m≥1 we haveΣ_(n≥2) Σ_(m≥1) ((x/m))^n .(1/n),≤Σ_(n≥2) (x^n /n).ζ(2)<∞ ,∀x∈]−1,1[ ⇒Σ_(n≥2) .Σ_(m≥1) ((x/m))^n .(1/n)=Σ_(m≥1) Σ_(n≥2) ((((x/m))^n )/n)=f(x) Σ_(k≥1) (a^k /k)=−ln(1−a)⇒Σ_(k≥2) (a^k /k)=−ln(1−a)−a f(x)=Σ_(m≥1) {−ln(1−(x/m))−(x/m)}=f(x) we have our sum=f(−(1/3)) Γ(x)=(1/x)Π_(k≥1) (((1+(1/k))^x )/(1+(x/k)))⇒(1/x)Π_(k≥1) .(e^(xln(1+(1/k))) /(1+(x/k)))=(1/x).Π_(k≥1) (e^(xln(1+(1/k))−(x/k)+(x/k)) /(1+(x/k))) =(1/x).Π_(k≥1) (e^(x(ln(1+(1/k))−(1/k))+(x/k)) /(1+(x/k)))=(1/x).e^(Σ_(k≥1) x(ln(1+(1/k))−(1/k))) .Π_(k≥1) (e^(x/k) /e^(ln(1+(x/k))) ) Σ_(k≥1) {ln(1+(1/k))−(1/k)}=−γ Euler macheronie Constent Γ(x)=(e^(−γx) /x).e^(Σ_(k≥1) {(x/k)−ln(1+(x/k))}) ⇒lnΓ(x)=−γx−ln(x)+Σ_(k≥1) {(x/k)−ln(1+(x/k))} ⇒Σ_(k≥1) {(x/k)−ln(1+(x/k))}=ln(Γ(x))+γx+ln(x) ⇒Σ_(k≥1) {−(x/k)−ln(1−(x/k))}=f(x)=ln(Γ(−x))−γx+ln(−x) S=f(−(1/3))=ln(Γ((1/3)))+(γ/3)+ln((1/3))=Σ_(n≥2) ((ζ(n))/(n(−3)^n ))](https://www.tinkutara.com/question/Q78666.png)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{n}\geqslant\mathrm{2}} {\sum}\frac{\zeta\left(\mathrm{n}\right)\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}=\underset{\mathrm{n}\geqslant\mathrm{2}} {\sum}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\underset{\mathrm{m}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{m}^{\mathrm{n}} } \\ $$$$=\underset{\mathrm{n}\geqslant\mathrm{2}} {\sum}.\underset{\mathrm{m}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{x}}{\mathrm{m}}\right)^{\mathrm{n}} .\frac{\mathrm{1}}{\mathrm{n}} \\ $$$$\forall\mathrm{n},\mathrm{m}\:,\mathrm{n}\geqslant\mathrm{2}\:\mathrm{and}\:\mathrm{m}\geqslant\mathrm{1}\: \\ $$$$\left.\mathrm{we}\:\mathrm{have}\underset{\mathrm{n}\geqslant\mathrm{2}} {\sum}\:\underset{\mathrm{m}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{x}}{\mathrm{m}}\right)^{\mathrm{n}} .\frac{\mathrm{1}}{\mathrm{n}},\leqslant\underset{\mathrm{n}\geqslant\mathrm{2}} {\sum}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}.\zeta\left(\mathrm{2}\right)<\infty\:\:,\forall\mathrm{x}\in\right]−\mathrm{1},\mathrm{1}\left[\right. \\ $$$$\Rightarrow\underset{\mathrm{n}\geqslant\mathrm{2}} {\sum}.\underset{\mathrm{m}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{x}}{\mathrm{m}}\right)^{\mathrm{n}} .\frac{\mathrm{1}}{\mathrm{n}}=\underset{\mathrm{m}\geqslant\mathrm{1}} {\sum}\underset{\mathrm{n}\geqslant\mathrm{2}} {\sum}\frac{\left(\frac{\mathrm{x}}{\mathrm{m}}\right)^{\mathrm{n}} }{\mathrm{n}}=\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{a}^{\mathrm{k}} }{\mathrm{k}}=−\mathrm{ln}\left(\mathrm{1}−\mathrm{a}\right)\Rightarrow\underset{\mathrm{k}\geqslant\mathrm{2}} {\sum}\frac{\mathrm{a}^{\mathrm{k}} }{\mathrm{k}}=−\mathrm{ln}\left(\mathrm{1}−\mathrm{a}\right)−\mathrm{a} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{m}\geqslant\mathrm{1}} {\sum}\left\{−\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{m}}\right)−\frac{\mathrm{x}}{\mathrm{m}}\right\}=\mathrm{f}\left(\mathrm{x}\right)\:\: \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{our}\:\mathrm{sum}=\mathrm{f}\left(−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\Gamma\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}}\underset{\mathrm{k}\geqslant\mathrm{1}} {\prod}\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}\right)^{\mathrm{x}} }{\mathrm{1}+\frac{\mathrm{x}}{\mathrm{k}}}\Rightarrow\frac{\mathrm{1}}{\mathrm{x}}\underset{\mathrm{k}\geqslant\mathrm{1}} {\prod}.\frac{\mathrm{e}^{\mathrm{xln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}\right)} }{\mathrm{1}+\frac{\mathrm{x}}{\mathrm{k}}}=\frac{\mathrm{1}}{\mathrm{x}}.\underset{\mathrm{k}\geqslant\mathrm{1}} {\prod}\frac{\mathrm{e}^{\mathrm{xln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}\right)−\frac{\mathrm{x}}{\mathrm{k}}+\frac{\mathrm{x}}{\mathrm{k}}} }{\mathrm{1}+\frac{\mathrm{x}}{\mathrm{k}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}}.\underset{\mathrm{k}\geqslant\mathrm{1}} {\prod}\frac{\mathrm{e}^{\mathrm{x}\left(\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}\right)−\frac{\mathrm{1}}{\mathrm{k}}\right)+\frac{\mathrm{x}}{\mathrm{k}}} }{\mathrm{1}+\frac{\mathrm{x}}{\mathrm{k}}}=\frac{\mathrm{1}}{\mathrm{x}}.\mathrm{e}^{\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\mathrm{x}\left(\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}\right)−\frac{\mathrm{1}}{\mathrm{k}}\right)} .\underset{\mathrm{k}\geqslant\mathrm{1}} {\prod}\frac{\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{k}}} }{\mathrm{e}^{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{k}}\right)} } \\ $$$$\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\left\{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}\right)−\frac{\mathrm{1}}{\mathrm{k}}\right\}=−\gamma\:\mathrm{Euler}\:\mathrm{macheronie}\:\mathrm{Constent} \\ $$$$\Gamma\left(\mathrm{x}\right)=\frac{\mathrm{e}^{−\gamma\mathrm{x}} }{\mathrm{x}}.\mathrm{e}^{\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\left\{\frac{\mathrm{x}}{\mathrm{k}}−\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{k}}\right)\right\}} \\ $$$$\Rightarrow\mathrm{ln}\Gamma\left(\mathrm{x}\right)=−\gamma\mathrm{x}−\mathrm{ln}\left(\mathrm{x}\right)+\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\left\{\frac{\mathrm{x}}{\mathrm{k}}−\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{k}}\right)\right\} \\ $$$$\Rightarrow\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\left\{\frac{\mathrm{x}}{\mathrm{k}}−\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{k}}\right)\right\}=\mathrm{ln}\left(\Gamma\left(\mathrm{x}\right)\right)+\gamma\mathrm{x}+\mathrm{ln}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\left\{−\frac{\mathrm{x}}{\mathrm{k}}−\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{k}}\right)\right\}=\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ln}\left(\Gamma\left(−\mathrm{x}\right)\right)−\gamma\mathrm{x}+\mathrm{ln}\left(−\mathrm{x}\right) \\ $$$$\mathrm{S}=\mathrm{f}\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)=\mathrm{ln}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right)+\frac{\gamma}{\mathrm{3}}+\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\underset{\mathrm{n}\geqslant\mathrm{2}} {\sum}\frac{\zeta\left(\mathrm{n}\right)}{\mathrm{n}\left(−\mathrm{3}\right)^{\mathrm{n}} } \\ $$$$ \\ $$$$ \\ $$
