Question Number 139023 by mohammad17 last updated on 21/Apr/21
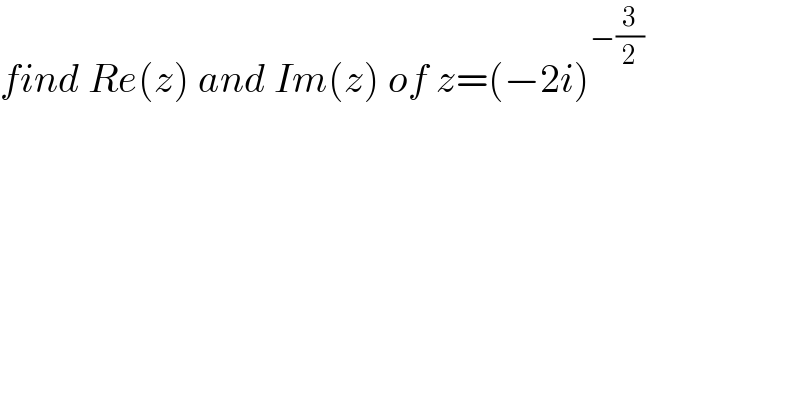
$${find}\:{Re}\left({z}\right)\:{and}\:{Im}\left({z}\right)\:{of}\:{z}=\left(−\mathrm{2}{i}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \\ $$
Answered by MJS_new last updated on 21/Apr/21
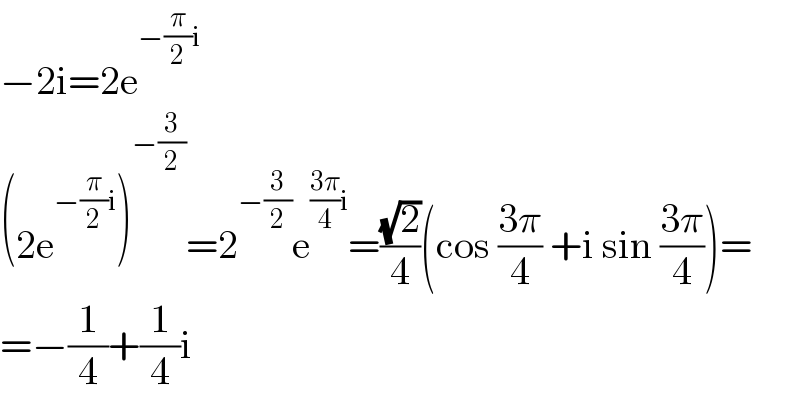
$$−\mathrm{2i}=\mathrm{2e}^{−\frac{\pi}{\mathrm{2}}\mathrm{i}} \\ $$$$\left(\mathrm{2e}^{−\frac{\pi}{\mathrm{2}}\mathrm{i}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} =\mathrm{2}^{−\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{e}^{\frac{\mathrm{3}\pi}{\mathrm{4}}\mathrm{i}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left(\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{4}}\:+\mathrm{i}\:\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{4}}\right)= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{i} \\ $$
