Question Number 75301 by vishalbhardwaj last updated on 09/Dec/19
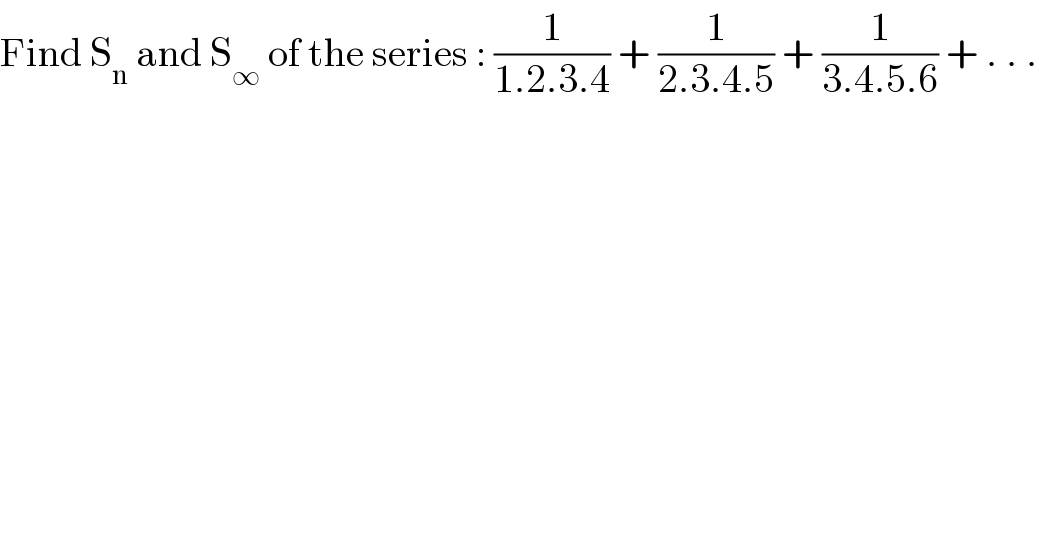
$$\mathrm{Find}\:\mathrm{S}_{\mathrm{n}} \:\mathrm{and}\:\mathrm{S}_{\infty} \:\mathrm{of}\:\mathrm{the}\:\mathrm{series}\::\:\frac{\mathrm{1}}{\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}}\:+\:\frac{\mathrm{1}}{\mathrm{2}.\mathrm{3}.\mathrm{4}.\mathrm{5}}\:+\:\frac{\mathrm{1}}{\mathrm{3}.\mathrm{4}.\mathrm{5}.\mathrm{6}}\:+\:.\:.\:. \\ $$
Commented by vishalbhardwaj last updated on 09/Dec/19

$$\mathrm{please}\:\mathrm{solve}\:\mathrm{this} \\ $$
Commented by vishalbhardwaj last updated on 09/Dec/19

$$\mathrm{please}\:\mathrm{solve}\:\mathrm{this} \\ $$
Commented by mind is power last updated on 09/Dec/19
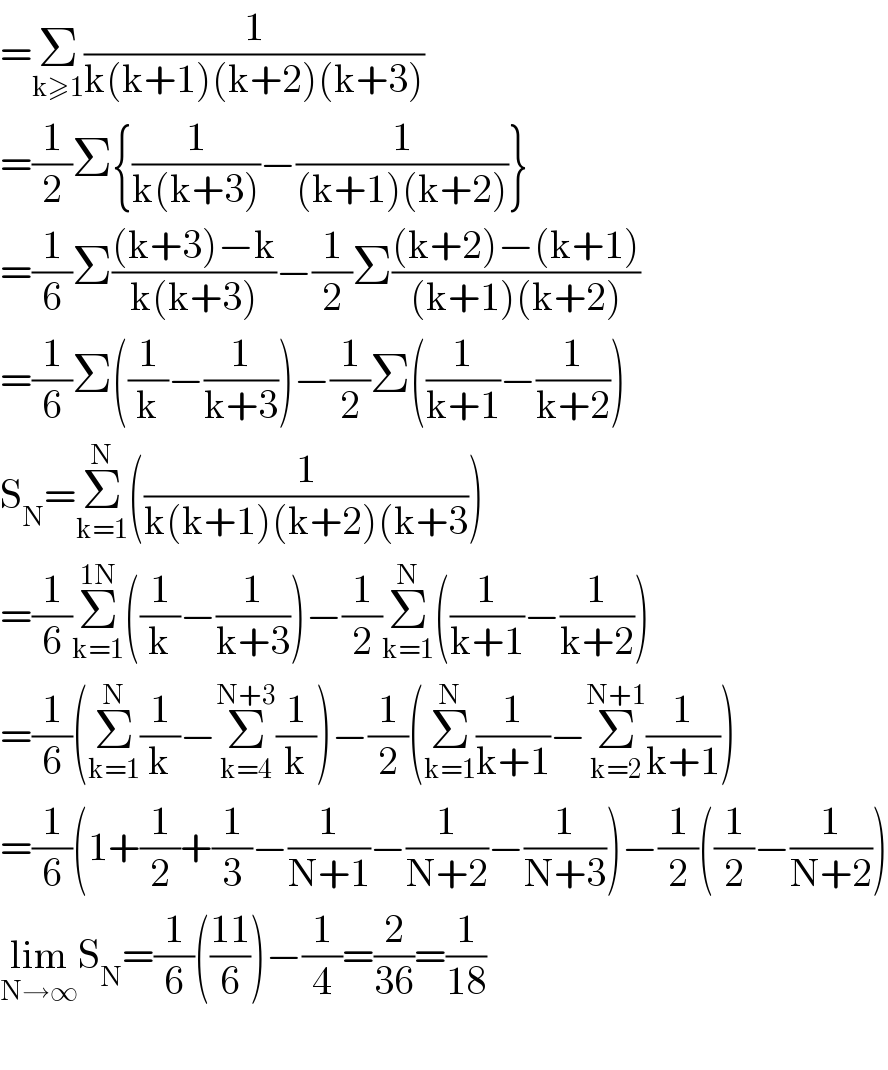
$$=\underset{\mathrm{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)\left(\mathrm{k}+\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\Sigma\left\{\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{3}\right)}−\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\Sigma\frac{\left(\mathrm{k}+\mathrm{3}\right)−\mathrm{k}}{\mathrm{k}\left(\mathrm{k}+\mathrm{3}\right)}−\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{\left(\mathrm{k}+\mathrm{2}\right)−\left(\mathrm{k}+\mathrm{1}\right)}{\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\Sigma\left(\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\Sigma\left(\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{2}}\right) \\ $$$$\mathrm{S}_{\mathrm{N}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)\left(\mathrm{k}+\mathrm{2}\right)\left(\mathrm{k}+\mathrm{3}\right.}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{1N}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left(\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}}−\underset{\mathrm{k}=\mathrm{4}} {\overset{\mathrm{N}+\mathrm{3}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}−\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{N}+\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{N}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{N}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{N}+\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{N}+\mathrm{2}}\right) \\ $$$$\underset{\mathrm{N}\rightarrow\infty} {\mathrm{lim}S}_{\mathrm{N}} =\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{11}}{\mathrm{6}}\right)−\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{2}}{\mathrm{36}}=\frac{\mathrm{1}}{\mathrm{18}} \\ $$$$ \\ $$
Commented by peter frank last updated on 09/Dec/19

$${thank}\:{you} \\ $$
