Menu Close

find-sin-20-

Tinku Tara 0 Comments
Pin




Question Number 68673 by mr W last updated on 14/Sep/19
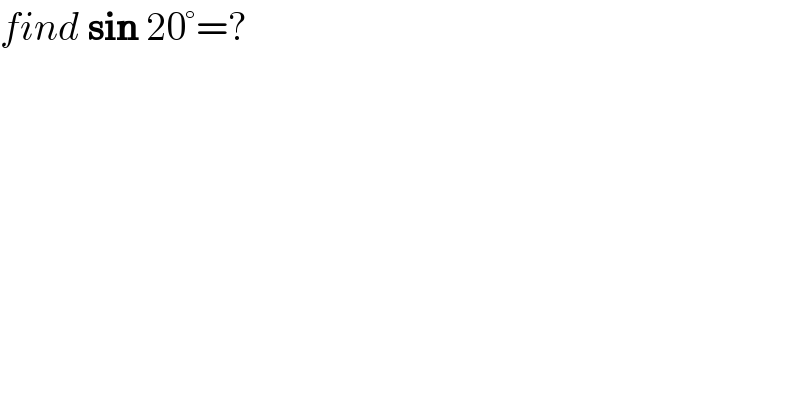
find sin 20°=?
$${find}\:\boldsymbol{\mathrm{sin}}\:\mathrm{20}°=? \\ $$
Commented by MJS last updated on 15/Sep/19
⇒ we cannot use this to get sin 1°, because sin 3° =(1/8)(1−(√3))(√(5+(√5)))−(1/(16))(1−(√5))(1+(√3))(√2) and sin 3° =3sin 1° −4sin^3 1° also leads to a super complex Cardano “solution” which is totally useless and the trigonometric method gives x_0 =sin ((1/3)arcsin (sin 3°)) =sin 1° x_1 =cos ((π/6)+(1/3)arcsin (sin 3°)) =cos 31° x_2 =−sin ((π/3)+(1/3)arcsin (sin 3°)) =−cos 29°
$$\Rightarrow\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{use}\:\mathrm{this}\:\mathrm{to}\:\mathrm{get}\:\mathrm{sin}\:\mathrm{1}°,\:\mathrm{because} \\ $$$$\mathrm{sin}\:\mathrm{3}°\:=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}−\sqrt{\mathrm{3}}\right)\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}−\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{1}−\sqrt{\mathrm{5}}\right)\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\sqrt{\mathrm{2}} \\ $$$$\mathrm{and} \\ $$$$\mathrm{sin}\:\mathrm{3}°\:=\mathrm{3sin}\:\mathrm{1}°\:−\mathrm{4sin}^{\mathrm{3}} \:\mathrm{1}° \\ $$$$\mathrm{also}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{super}\:\mathrm{complex}\:\mathrm{Cardano} \\ $$$$“\mathrm{solution}''\:\mathrm{which}\:\mathrm{is}\:\mathrm{totally}\:\mathrm{useless} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{trigonometric}\:\mathrm{method}\:\mathrm{gives} \\ $$$${x}_{\mathrm{0}} =\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\left(\mathrm{sin}\:\mathrm{3}°\right)\right)\:=\mathrm{sin}\:\mathrm{1}° \\ $$$${x}_{\mathrm{1}} =\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\left(\mathrm{sin}\:\mathrm{3}°\right)\right)\:=\mathrm{cos}\:\mathrm{31}° \\ $$$${x}_{\mathrm{2}} =−\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\left(\mathrm{sin}\:\mathrm{3}°\right)\right)\:=−\mathrm{cos}\:\mathrm{29}° \\ $$
Commented by Prithwish sen last updated on 15/Sep/19
Thanks Sir.
$$\mathrm{Thanks}\:\mathrm{Sir}. \\ $$
Commented by MJS last updated on 14/Sep/19
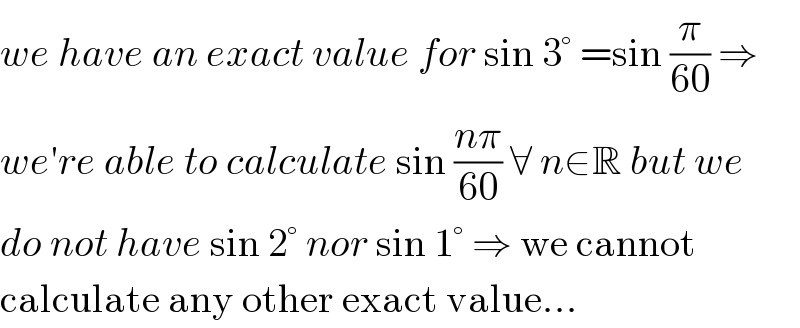
we have an exact value for sin 3° =sin (π/(60)) ⇒ we′re able to calculate sin ((nπ)/(60)) ∀ n∈R but we do not have sin 2° nor sin 1° ⇒ we cannot calculate any other exact value...
$${we}\:{have}\:{an}\:{exact}\:{value}\:{for}\:\mathrm{sin}\:\mathrm{3}°\:=\mathrm{sin}\:\frac{\pi}{\mathrm{60}}\:\Rightarrow \\ $$$${we}'{re}\:{able}\:{to}\:{calculate}\:\mathrm{sin}\:\frac{{n}\pi}{\mathrm{60}}\:\forall\:{n}\in\mathbb{R}\:{but}\:{we} \\ $$$${do}\:{not}\:{have}\:\mathrm{sin}\:\mathrm{2}°\:{nor}\:\mathrm{sin}\:\mathrm{1}°\:\Rightarrow\:\mathrm{we}\:\mathrm{cannot} \\ $$$$\mathrm{calculate}\:\mathrm{any}\:\mathrm{other}\:\mathrm{exact}\:\mathrm{value}… \\ $$
Commented by Maclaurin Stickker last updated on 15/Sep/19
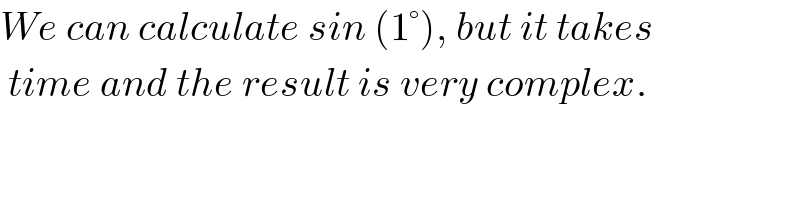
We can calculate sin (1°), but it takes time and the result is very complex.
$${We}\:{can}\:{calculate}\:{sin}\:\left(\mathrm{1}°\right),\:{but}\:{it}\:{takes} \\ $$$$\:{time}\:{and}\:{the}\:{result}\:{is}\:{very}\:{complex}. \\ $$
Commented by mr W last updated on 15/Sep/19
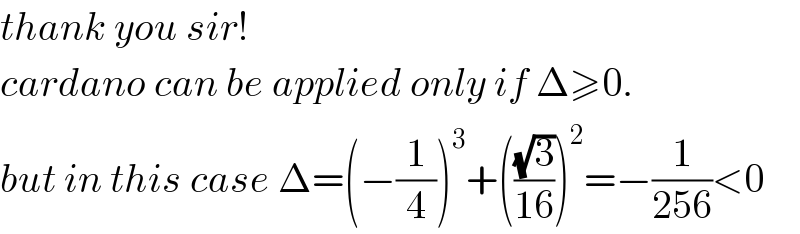
thank you sir! cardano can be applied only if Δ≥0. but in this case Δ=(−(1/4))^3 +(((√3)/(16)))^2 =−(1/(256))<0
$${thank}\:{you}\:{sir}! \\ $$$${cardano}\:{can}\:{be}\:{applied}\:{only}\:{if}\:\Delta\geqslant\mathrm{0}. \\ $$$${but}\:{in}\:{this}\:{case}\:\Delta=\left(−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{16}}\right)^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{256}}<\mathrm{0} \\ $$
Commented by Prithwish sen last updated on 15/Sep/19
Sin60^° =3Sin20^° −4Sin^3 20^° Let Sin20^° =x ∴ ((√3)/2) = 3x−4x^3 x^3 −(3/4)x+((√3)/8) =0 By Cardano′s method for x^3 −3px−2q=0 x=^3 (√(q+(√(q^2 −p^3 )))) +^3 (√(q−(√(q^2 −p^3 )))) we get p = (1/4) and q = −((√3)/(16)) x =^3 (√(((−(√3))/(16))+(√((3/(256))−(1/(64)))))) +^3 (√(((−(√3))/(16)) + (√((3/(256)) −(1/(64)))))) =^3 (√((−(√(3+))i)/(16))) +^3 (√((−(√3)−i)/(16))) Sir,waiting for your valuable comment.
$$\mathrm{Sin60}^{°} =\mathrm{3Sin20}^{°} −\mathrm{4Sin}^{\mathrm{3}} \mathrm{20}^{°} \\ $$$$\mathrm{Let}\:\mathrm{Sin20}^{°} =\mathrm{x} \\ $$$$\therefore\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:\mathrm{3x}−\mathrm{4x}^{\mathrm{3}} \\ $$$$\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{4}}\mathrm{x}+\frac{\sqrt{\mathrm{3}}}{\mathrm{8}}\:=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{By}}\:\boldsymbol{\mathrm{Cardano}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{method}}\:\boldsymbol{\mathrm{for}} \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{3}} −\mathrm{3}\boldsymbol{\mathrm{px}}−\mathrm{2}\boldsymbol{\mathrm{q}}=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{x}}=^{\mathrm{3}} \sqrt{\boldsymbol{\mathrm{q}}+\sqrt{\boldsymbol{\mathrm{q}}^{\mathrm{2}} −\boldsymbol{\mathrm{p}}^{\mathrm{3}} }}\:+^{\mathrm{3}} \sqrt{\boldsymbol{\mathrm{q}}−\sqrt{\boldsymbol{\mathrm{q}}^{\mathrm{2}} −\boldsymbol{\mathrm{p}}^{\mathrm{3}} }} \\ $$$$\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{get}}\:\:\boldsymbol{\mathrm{p}}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{q}}\:=\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{16}} \\ $$$$\boldsymbol{\mathrm{x}}\:=\:^{\mathrm{3}} \sqrt{\frac{−\sqrt{\mathrm{3}}}{\mathrm{16}}+\sqrt{\frac{\mathrm{3}}{\mathrm{256}}−\frac{\mathrm{1}}{\mathrm{64}}}}\:+^{\mathrm{3}} \sqrt{\frac{−\sqrt{\mathrm{3}}}{\mathrm{16}}\:+\:\sqrt{\frac{\mathrm{3}}{\mathrm{256}}\:−\frac{\mathrm{1}}{\mathrm{64}}}} \\ $$$$\:\:\:\:\:\:=\:^{\mathrm{3}} \sqrt{\frac{−\sqrt{\mathrm{3}+}\boldsymbol{\mathrm{i}}}{\mathrm{16}}}\:+^{\mathrm{3}} \sqrt{\frac{−\sqrt{\mathrm{3}}−\boldsymbol{\mathrm{i}}}{\mathrm{16}}} \\ $$$$\boldsymbol{\mathrm{Sir}},\boldsymbol{\mathrm{waiting}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{valuable}}\:\boldsymbol{\mathrm{comment}}. \\ $$
Commented by Prithwish sen last updated on 15/Sep/19
Thank you Sir!
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}! \\ $$
Commented by MJS last updated on 15/Sep/19
using Cardano is possible but (1) we have to approximate all 3 solutions to find which is the right one and (2) the written out solution is not useable. but also the trigonometric method doesn′t satisfy sometimes (x−2)(x+3)(x−5)=0 x^3 −4x^2 −11x+30=0 x=t+(4/3) t^3 −((49)/3)t+((286)/(27))=0 Cardano leads to u=((−((143)/(27))+((20(√3)i)/3)))^(1/3) ; v=((−((143)/(27))−((20(√3)i)/3)))^(1/3) x_1 =u+v x_2 =(−(1/2)−(((√3)i)/2))u+(−(1/2)+(((√3)i)/2))v x_3 =(−(1/2)+(((√3)i)/2))u+(−(1/2)−(((√3)i)/2))v and I don′t think it′s possible to handle these or to analytically show x_1 =5; x_2 =2; x_3 =−3 the trigonometric method gives x_0 =(4/3)+((14)/3)sin ((1/3)arcsin ((143)/(343))) x_1 =(4/3)+((14)/3)cos ((π/6)+(1/3)arcsin ((143)/(343))) x_2 =(4/3)−((14)/3)sin ((π/3)+(1/3)arcsin ((143)/(343))) again, try to show x_0 =2; x_1 =5; x_2 =−3 as we see, the actual solutions can be well hidden
$$\mathrm{using}\:\mathrm{Cardano}\:\mathrm{is}\:\mathrm{possible}\:\mathrm{but}\:\left(\mathrm{1}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{to} \\ $$$$\mathrm{approximate}\:\mathrm{all}\:\mathrm{3}\:\mathrm{solutions}\:\mathrm{to}\:\mathrm{find}\:\mathrm{which}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{right}\:\mathrm{one}\:\mathrm{and}\:\left(\mathrm{2}\right)\:\mathrm{the}\:\mathrm{written}\:\mathrm{out}\:\mathrm{solution} \\ $$$$\mathrm{is}\:\mathrm{not}\:\mathrm{useable}.\:\mathrm{but}\:\mathrm{also}\:\mathrm{the}\:\mathrm{trigonometric} \\ $$$$\mathrm{method}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{satisfy}\:\mathrm{sometimes} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}+\mathrm{3}\right)\left({x}−\mathrm{5}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{11}{x}+\mathrm{30}=\mathrm{0} \\ $$$${x}={t}+\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{49}}{\mathrm{3}}{t}+\frac{\mathrm{286}}{\mathrm{27}}=\mathrm{0} \\ $$$$\mathrm{Cardano}\:\mathrm{leads}\:\mathrm{to} \\ $$$${u}=\sqrt[{\mathrm{3}}]{−\frac{\mathrm{143}}{\mathrm{27}}+\frac{\mathrm{20}\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{3}}};\:{v}=\sqrt[{\mathrm{3}}]{−\frac{\mathrm{143}}{\mathrm{27}}−\frac{\mathrm{20}\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{3}}} \\ $$$${x}_{\mathrm{1}} ={u}+{v} \\ $$$${x}_{\mathrm{2}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{2}}\right){u}+\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{2}}\right){v} \\ $$$${x}_{\mathrm{3}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{2}}\right){u}+\left(−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{2}}\right){v} \\ $$$$\mathrm{and}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{handle}\:\mathrm{these} \\ $$$$\mathrm{or}\:\mathrm{to}\:\mathrm{analytically}\:\mathrm{show}\:{x}_{\mathrm{1}} =\mathrm{5};\:{x}_{\mathrm{2}} =\mathrm{2};\:{x}_{\mathrm{3}} =−\mathrm{3} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{trigonometric}\:\mathrm{method}\:\mathrm{gives} \\ $$$${x}_{\mathrm{0}} =\frac{\mathrm{4}}{\mathrm{3}}+\frac{\mathrm{14}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{143}}{\mathrm{343}}\right) \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{4}}{\mathrm{3}}+\frac{\mathrm{14}}{\mathrm{3}}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{143}}{\mathrm{343}}\right) \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{14}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{143}}{\mathrm{343}}\right) \\ $$$$\mathrm{again},\:\mathrm{try}\:\mathrm{to}\:\mathrm{show}\:{x}_{\mathrm{0}} =\mathrm{2};\:{x}_{\mathrm{1}} =\mathrm{5};\:{x}_{\mathrm{2}} =−\mathrm{3} \\ $$$$ \\ $$$$\mathrm{as}\:\mathrm{we}\:\mathrm{see},\:\mathrm{the}\:\mathrm{actual}\:\mathrm{solutions}\:\mathrm{can}\:\mathrm{be}\:\mathrm{well}\:\mathrm{hidden} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *