Question Number 1018 by prakash jain last updated on 15/May/15
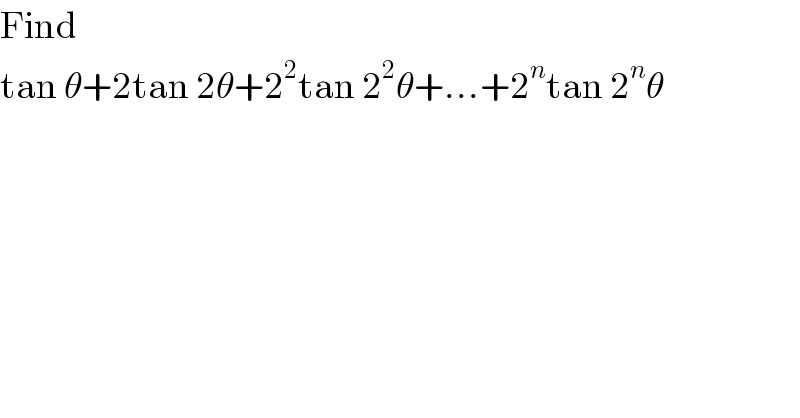
$$\mathrm{Find} \\ $$$$\mathrm{tan}\:\theta+\mathrm{2tan}\:\mathrm{2}\theta+\mathrm{2}^{\mathrm{2}} \mathrm{tan}\:\mathrm{2}^{\mathrm{2}} \theta+…+\mathrm{2}^{{n}} \mathrm{tan}\:\mathrm{2}^{{n}} \theta \\ $$
Answered by prakash jain last updated on 16/May/15
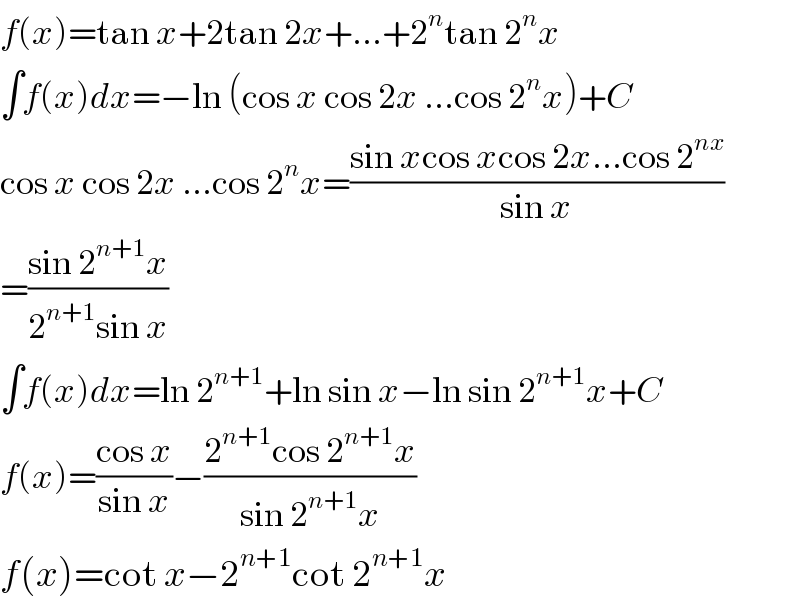
$${f}\left({x}\right)=\mathrm{tan}\:{x}+\mathrm{2tan}\:\mathrm{2}{x}+…+\mathrm{2}^{{n}} \mathrm{tan}\:\mathrm{2}^{{n}} {x} \\ $$$$\int{f}\left({x}\right){dx}=−\mathrm{ln}\:\left(\mathrm{cos}\:{x}\:\mathrm{cos}\:\mathrm{2}{x}\:…\mathrm{cos}\:\mathrm{2}^{{n}} {x}\right)+{C} \\ $$$$\mathrm{cos}\:{x}\:\mathrm{cos}\:\mathrm{2}{x}\:…\mathrm{cos}\:\mathrm{2}^{{n}} {x}=\frac{\mathrm{sin}\:{x}\mathrm{cos}\:{x}\mathrm{cos}\:\mathrm{2}{x}…\mathrm{cos}\:\mathrm{2}^{{nx}} }{\mathrm{sin}\:{x}} \\ $$$$=\frac{\mathrm{sin}\:\mathrm{2}^{{n}+\mathrm{1}} {x}}{\mathrm{2}^{{n}+\mathrm{1}} \mathrm{sin}\:{x}} \\ $$$$\int{f}\left({x}\right){dx}=\mathrm{ln}\:\mathrm{2}^{{n}+\mathrm{1}} +\mathrm{ln}\:\mathrm{sin}\:{x}−\mathrm{ln}\:\mathrm{sin}\:\mathrm{2}^{{n}+\mathrm{1}} {x}+{C} \\ $$$${f}\left({x}\right)=\frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}}−\frac{\mathrm{2}^{{n}+\mathrm{1}} \mathrm{cos}\:\mathrm{2}^{{n}+\mathrm{1}} {x}}{\mathrm{sin}\:\mathrm{2}^{{n}+\mathrm{1}} {x}} \\ $$$${f}\left({x}\right)=\mathrm{cot}\:{x}−\mathrm{2}^{{n}+\mathrm{1}} \mathrm{cot}\:\mathrm{2}^{{n}+\mathrm{1}} {x} \\ $$
