Question Number 67106 by mhmd last updated on 22/Aug/19

$${find}\:{the}\:{area}\:{abounded}\:{y}=\sqrt{{x}} \\ $$$${afind}\:{y}={x}−\mathrm{2}? \\ $$
Commented by kaivan.ahmadi last updated on 24/Aug/19
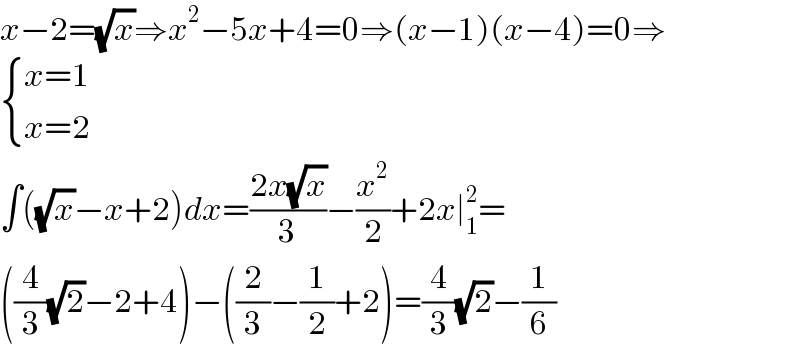
$${x}−\mathrm{2}=\sqrt{{x}}\Rightarrow{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{4}=\mathrm{0}\Rightarrow\left({x}−\mathrm{1}\right)\left({x}−\mathrm{4}\right)=\mathrm{0}\Rightarrow \\ $$$$\begin{cases}{{x}=\mathrm{1}}\\{{x}=\mathrm{2}}\end{cases} \\ $$$$\int\left(\sqrt{{x}}−{x}+\mathrm{2}\right){dx}=\frac{\mathrm{2}{x}\sqrt{{x}}}{\mathrm{3}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}{x}\mid_{\mathrm{1}} ^{\mathrm{2}} = \\ $$$$\left(\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\mathrm{2}}−\mathrm{2}+\mathrm{4}\right)−\left(\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}\right)=\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6}} \\ $$
