Question Number 67618 by mhmd last updated on 29/Aug/19
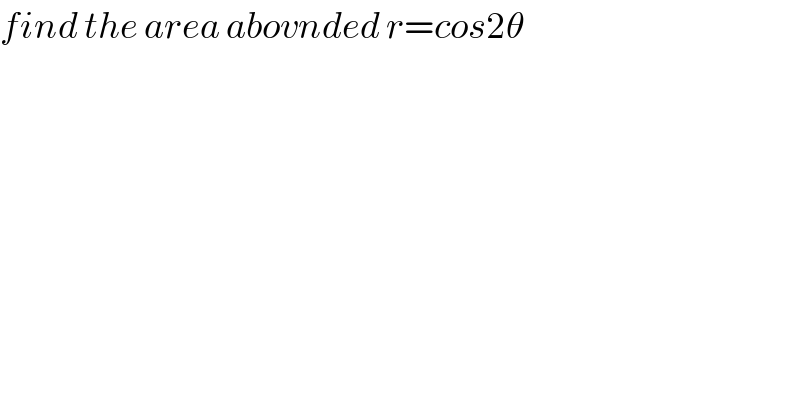
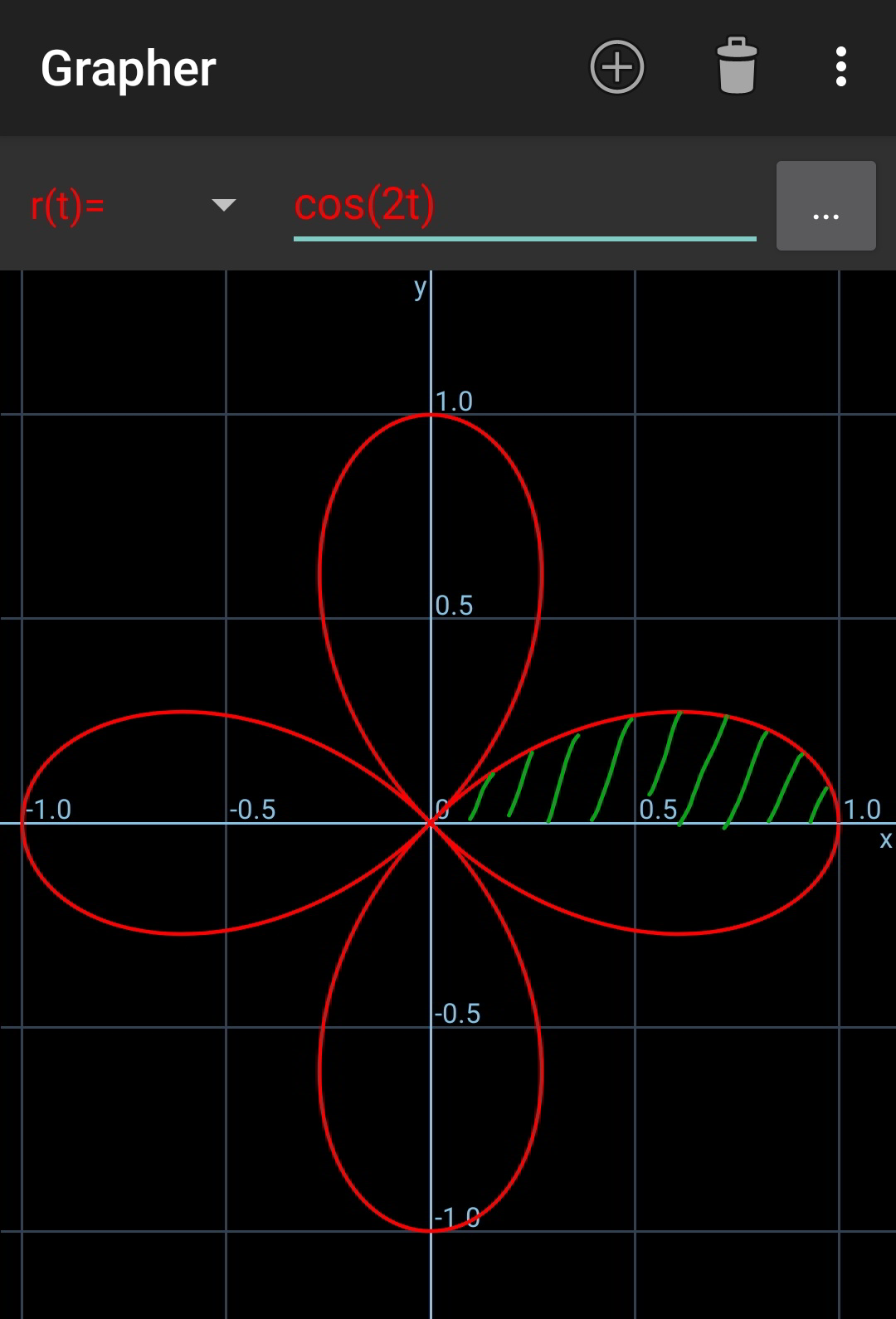
$${find}\:{the}\:{area}\:{abovnded}\:{r}={cos}\mathrm{2}\theta \\ $$
Answered by mr W last updated on 29/Aug/19
![A=8∫_0 ^(π/4) ((r^2 dθ)/2) =8∫_0 ^(π/4) ((cos^2 2θ dθ)/2) =2∫_0 ^(π/4) 2cos^2 2θ dθ =2∫_0 ^(π/4) (1+cos 4θ) dθ =2[θ+((sin 4θ)/4)]_0 ^(π/4) =2×(π/4) =(π/2)](https://www.tinkutara.com/question/Q67621.png)
$${A}=\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{r}^{\mathrm{2}} {d}\theta}{\mathrm{2}} \\ $$$$=\mathrm{8}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\theta\:{d}\theta}{\mathrm{2}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{2cos}^{\mathrm{2}} \:\mathrm{2}\theta\:{d}\theta \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{4}\theta\right)\:{d}\theta \\ $$$$=\mathrm{2}\left[\theta+\frac{\mathrm{sin}\:\mathrm{4}\theta}{\mathrm{4}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\mathrm{2}×\frac{\pi}{\mathrm{4}} \\ $$$$=\frac{\pi}{\mathrm{2}} \\ $$
Commented by mr W last updated on 29/Aug/19