Question Number 72401 by Learner-123 last updated on 28/Oct/19

$${Find}\:{the}\:{area}\:{bounded}\:{by}\:{one}\:{leaf}\:{of} \\ $$$${the}\:{rose}\:{r}\:=\:\mathrm{12cos}\:\left(\mathrm{3}\theta\right). \\ $$
Answered by ajfour last updated on 28/Oct/19
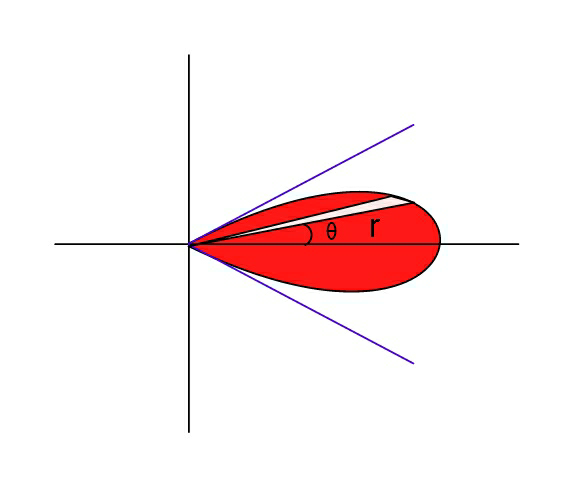
Commented by ajfour last updated on 28/Oct/19

$${A}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{6}} {a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{3}\theta{d}\theta \\ $$$$\:\:\:=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\int_{\mathrm{0}} ^{\:\pi/\mathrm{6}} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{6}\theta\right){d}\theta \\ $$$$\:\:\:=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{6}}\right)\:\: \\ $$$${for}\:{a}=\mathrm{12} \\ $$$$\:\:{A}=\mathrm{12}\pi\:. \\ $$
Commented by Learner-123 last updated on 28/Oct/19

$${how}\:,\:{upper}\:{limit}\:{is}\:\theta=\frac{\pi}{\mathrm{6}}? \\ $$
Commented by ajfour last updated on 28/Oct/19

$${for}\:\theta=\frac{\pi}{\mathrm{6}}\:,\:\:\mathrm{cos}\:\mathrm{3}\theta=\mathrm{cos}\:\frac{\pi}{\mathrm{2}}=\mathrm{0} \\ $$$${it}\:{boundary}\:{closes}\:{r}=\mathrm{0}. \\ $$$${Angular}\:{range}\:{of}\:{above}\:{petal}\:{is} \\ $$$$\:\:\theta=−\frac{\pi}{\mathrm{6}}\:\:{to}\:\:\theta=\frac{\pi}{\mathrm{6}}\:.\:{Is}\:{that}\:{all}\:{right}? \\ $$$${A}=\int_{−\pi/\mathrm{6}} ^{\:\pi/\mathrm{6}} \left(\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\right){d}\theta\:=\:\int_{\mathrm{0}} ^{\:\pi/\mathrm{6}} {r}^{\mathrm{2}} {d}\theta\:. \\ $$
Commented by Learner-123 last updated on 28/Oct/19

$${thank}\:{you}\:{sir}! \\ $$
