Find-the-area-of-the-region-between-the-graphs-of-f-x-3x-3-x-2-10x-and-g-x-x-3-2x-

Question Number 12139 by tawa last updated on 14/Apr/17

Find the area of the region between the graphs of f (x) = {3 x}^{3} - x^{2} - 10 x

and g (x) = - x^{3} + 2 x

Answered by mrW1 last updated on 15/Apr/17

3 x^{3} - x^{2} - 10 x = - x^{3} + 2 x

4 x^{3} - x^{2} - 12 x = 0

x (4 x^{2} - x - 12) = 0

x = 0

4 x^{2} - x - 12 = 0

x = \frac{1 \pm \sqrt{1 + 4 \times 4 \times 12}}{2 \times 4} = \frac{1 \pm \sqrt{193}}{8}

x_{1} = \frac{1 - \sqrt{193}}{8}

x_{2} = 0

x_{3} = \frac{1 + \sqrt{193}}{8}

A = \int_{a}^{b} [f (x) - g (x)] d x

= \int_{a}^{b} (3 x^{3} - x^{2} - 10 x + x^{3} - 2 x) d x

= \int_{a}^{b} (4 x^{3} - x^{2} - 12 x) d x

= {[x^{4} - \frac{x^{3}}{3} - 6 x^{2}]}_{a}^{b}

A_{1} =∣ {[x^{4} - \frac{x^{3}}{3} - 6 x^{2}]}_{x_{1}}^{0} ∣

A_{1} =∣ {(\frac{1 - \sqrt{193}}{8})}^{4} - \frac{1}{3} {(\frac{1 - \sqrt{193}}{8})}^{3} - 6 {(\frac{1 - \sqrt{193}}{8})}^{2} ∣

=∣ {(\frac{1 - \sqrt{193}}{8})}^{2} [{(\frac{1 - \sqrt{193}}{8})}^{2} - \frac{1}{3} (\frac{1 - \sqrt{193}}{8}) - 6] ∣

A_{2} =∣ {[x^{4} - \frac{x^{3}}{3} - 6 x^{2}]}_{0}^{x_{2}} ∣

A_{2} =∣ {(\frac{1 + \sqrt{193}}{8})}^{4} - \frac{1}{3} {(\frac{1 + \sqrt{193}}{8})}^{3} - 6 {(\frac{1 + \sqrt{193}}{8})}^{2} ∣

=∣ {(\frac{1 + \sqrt{193}}{8})}^{2} [{(\frac{1 + \sqrt{193}}{8})}^{2} - \frac{1}{3} (\frac{1 + \sqrt{193}}{8}) - 6] ∣

A_{1} + A_{2} = \frac{14113}{768} \approx 18.376

Commented by tawa last updated on 14/Apr/17

Wow, i really appreciate sir .

Commented by tawa last updated on 14/Apr/17

God bless you sir

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 14/Apr/17

Commented by tawa last updated on 14/Apr/17

God bless you sir

Commented by chux last updated on 15/Apr/17

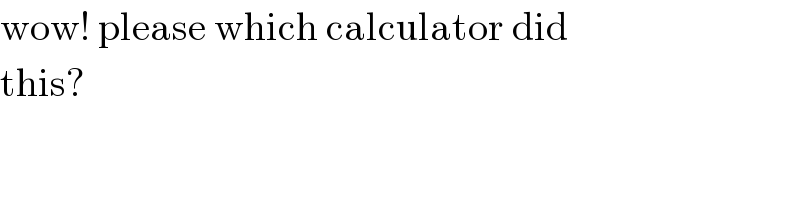
wow! please which calculator did

this ?

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/Apr/17

h e l l o . F S C c a l c u l a t o r .

Commented by chux last updated on 16/Apr/17

thanks

Facebook Tweet Pin