Question Number 9731 by tawakalitu last updated on 29/Dec/16
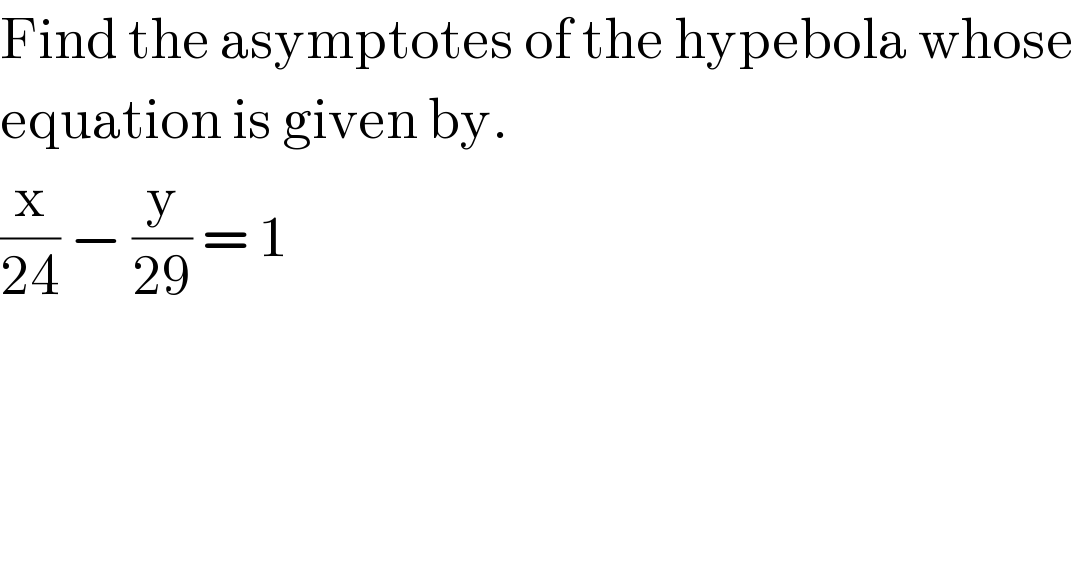
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{asymptotes}\:\mathrm{of}\:\mathrm{the}\:\mathrm{hypebola}\:\mathrm{whose} \\ $$$$\mathrm{equation}\:\mathrm{is}\:\mathrm{given}\:\mathrm{by}. \\ $$$$\frac{\mathrm{x}}{\mathrm{24}}\:−\:\frac{\mathrm{y}}{\mathrm{29}}\:=\:\mathrm{1} \\ $$
Commented by geovane10math last updated on 29/Dec/16
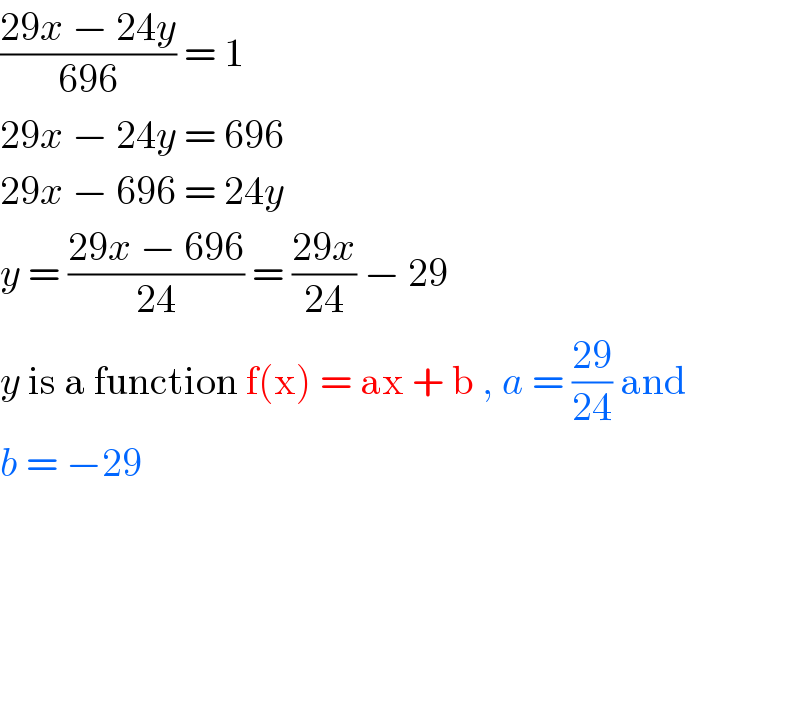
$$\frac{\mathrm{29}{x}\:−\:\mathrm{24}{y}}{\mathrm{696}}\:=\:\mathrm{1} \\ $$$$\mathrm{29}{x}\:−\:\mathrm{24}{y}\:=\:\mathrm{696} \\ $$$$\mathrm{29}{x}\:−\:\mathrm{696}\:=\:\mathrm{24}{y} \\ $$$${y}\:=\:\frac{\mathrm{29}{x}\:−\:\mathrm{696}}{\mathrm{24}}\:=\:\frac{\mathrm{29}{x}}{\mathrm{24}}\:−\:\mathrm{29} \\ $$$${y}\:\mathrm{is}\:\mathrm{a}\:\mathrm{function}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{ax}\:+\:\mathrm{b}\:,\:{a}\:=\:\frac{\mathrm{29}}{\mathrm{24}}\:\mathrm{and}\: \\ $$$${b}\:=\:−\mathrm{29} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by sandy_suhendra last updated on 29/Dec/16
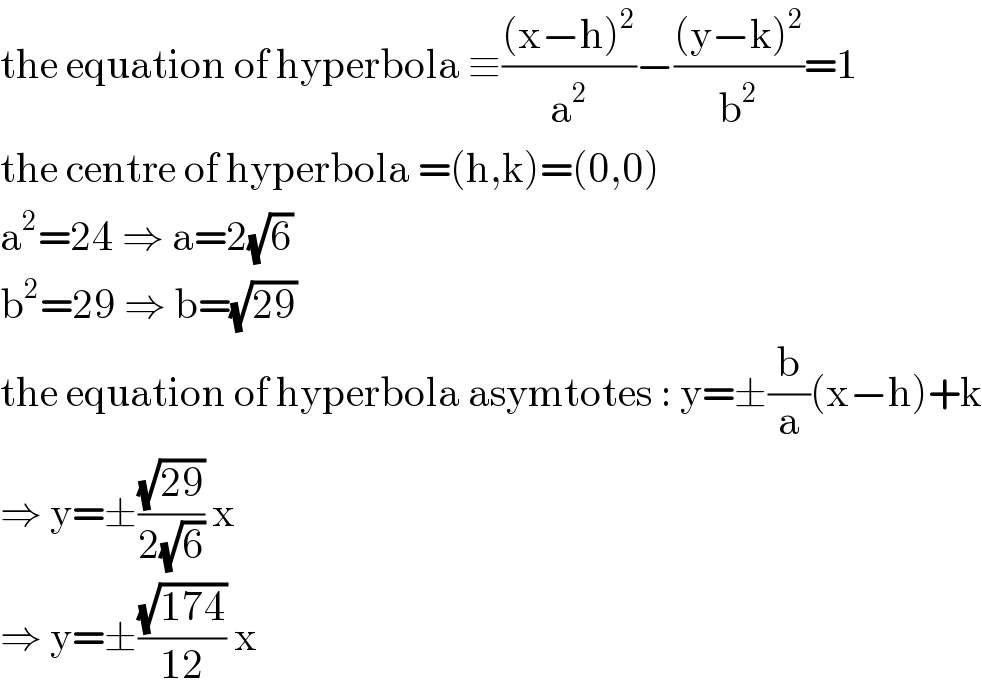
$$\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{hyperbola}\:\equiv\frac{\left(\mathrm{x}−\mathrm{h}\right)^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }−\frac{\left(\mathrm{y}−\mathrm{k}\right)^{\mathrm{2}} }{\mathrm{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{centre}\:\mathrm{of}\:\mathrm{hyperbola}\:=\left(\mathrm{h},\mathrm{k}\right)=\left(\mathrm{0},\mathrm{0}\right) \\ $$$$\mathrm{a}^{\mathrm{2}} =\mathrm{24}\:\Rightarrow\:\mathrm{a}=\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\mathrm{b}^{\mathrm{2}} =\mathrm{29}\:\Rightarrow\:\mathrm{b}=\sqrt{\mathrm{29}} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{hyperbola}\:\mathrm{asymtotes}\::\:\mathrm{y}=\pm\frac{\mathrm{b}}{\mathrm{a}}\left(\mathrm{x}−\mathrm{h}\right)+\mathrm{k} \\ $$$$\Rightarrow\:\mathrm{y}=\pm\frac{\sqrt{\mathrm{29}}}{\mathrm{2}\sqrt{\mathrm{6}}}\:\mathrm{x} \\ $$$$\Rightarrow\:\mathrm{y}=\pm\frac{\sqrt{\mathrm{174}}}{\mathrm{12}}\:\mathrm{x} \\ $$
Commented by tawakalitu last updated on 29/Dec/16
$$\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
