Question Number 78119 by jagoll last updated on 14/Jan/20
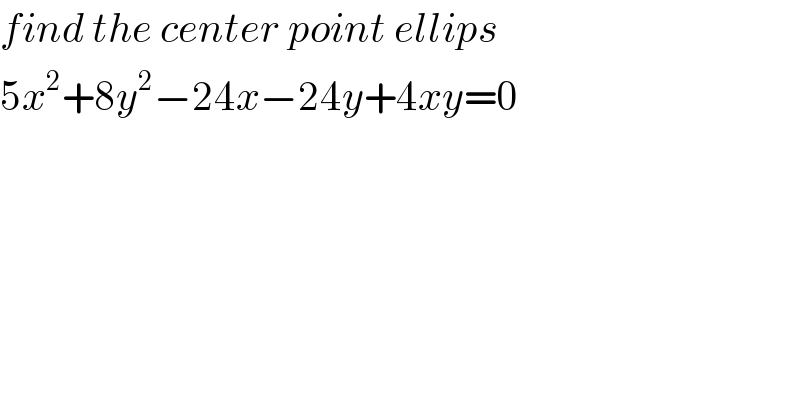
$${find}\:{the}\:{center}\:{point}\:{ellips} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{8}{y}^{\mathrm{2}} −\mathrm{24}{x}−\mathrm{24}{y}+\mathrm{4}{xy}=\mathrm{0} \\ $$
Commented by jagoll last updated on 14/Jan/20
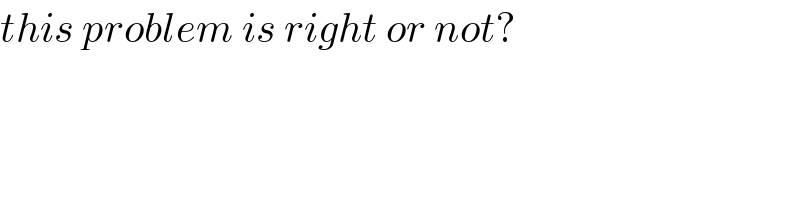
$${this}\:{problem}\:{is}\:{right}\:{or}\:{not}? \\ $$
Commented by mr W last updated on 14/Jan/20
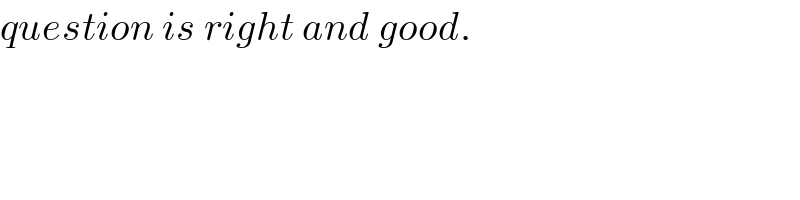
$${question}\:{is}\:{right}\:{and}\:{good}. \\ $$
Commented by MJS last updated on 14/Jan/20
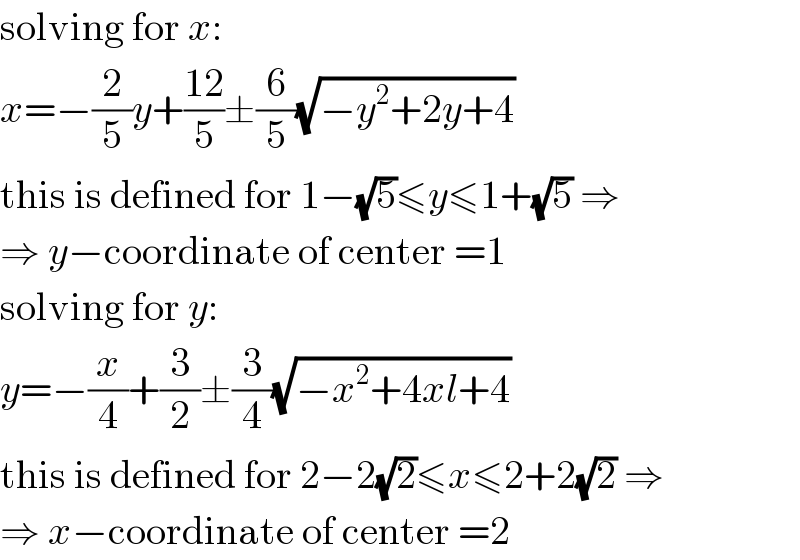
$$\mathrm{solving}\:\mathrm{for}\:{x}: \\ $$$${x}=−\frac{\mathrm{2}}{\mathrm{5}}{y}+\frac{\mathrm{12}}{\mathrm{5}}\pm\frac{\mathrm{6}}{\mathrm{5}}\sqrt{−{y}^{\mathrm{2}} +\mathrm{2}{y}+\mathrm{4}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:\mathrm{1}−\sqrt{\mathrm{5}}\leqslant{y}\leqslant\mathrm{1}+\sqrt{\mathrm{5}}\:\Rightarrow \\ $$$$\Rightarrow\:{y}−\mathrm{coordinate}\:\mathrm{of}\:\mathrm{center}\:=\mathrm{1} \\ $$$$\mathrm{solving}\:\mathrm{for}\:{y}: \\ $$$${y}=−\frac{{x}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{2}}\pm\frac{\mathrm{3}}{\mathrm{4}}\sqrt{−{x}^{\mathrm{2}} +\mathrm{4}{xl}+\mathrm{4}} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}\leqslant{x}\leqslant\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}\:\Rightarrow \\ $$$$\Rightarrow\:{x}−\mathrm{coordinate}\:\mathrm{of}\:\mathrm{center}\:=\mathrm{2} \\ $$
Commented by jagoll last updated on 14/Jan/20

$${thanks}\:{sir}\: \\ $$
Commented by jagoll last updated on 14/Jan/20
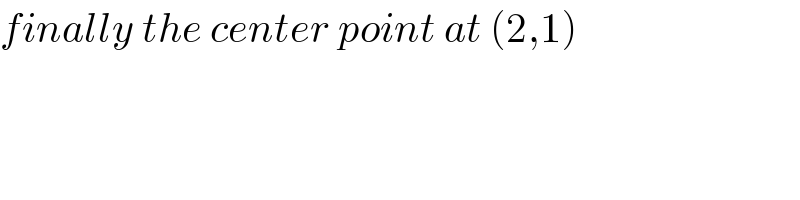
$${finally}\:{the}\:{center}\:{point}\:{at}\:\left(\mathrm{2},\mathrm{1}\right) \\ $$
Commented by MJS last updated on 14/Jan/20

$$\mathrm{yes} \\ $$
Answered by mr W last updated on 15/Jan/20
![if you don′t like to learn too many formulas, you can determine the parameters of the ellipse in following way: step 1: determine center point that means to determine the range of x and y ordinates. (see also sir MJS′ post) we form eqn. as quadratic eqn. w.r.t. y: 8y^2 +4(x−6)y+5x^2 −24x=0 Δ=4^2 (x−6)^2 −4×8×(5x^2 −24x)≥0 (x−6)^2 −2(5x^2 −24x)≥0 −x^2 +4x+4≥0 x^2 −4x−4≤0 (x−2)^2 −8≤0 ⇒2−2(√2)≤x≤2+2(√2) ⇒x_C =2 we form eqn. as quadratic eqn. w.r.t. x: 5x^2 +4(y−6)x+8y^2 −24y=0 Δ=4^2 (y−6)^2 −4×5(8y^2 −24y)≥0 (y−6)^2 −5(2y^2 −6y)≥0 −y^2 +2y+4≥0 y^2 −2y−4≤0 (y−1)^2 −5≤0 ⇒1−(√5)≤y≤1+(√5) ⇒y_C =1 ⇒center point of ellipse is C(2,1) step 2: make the center point as origin replace x with x+x_C and y with y+y_C in the eqn. 5(x+2)^2 +8(y+1)^2 −24(x+2)−24(y+1)+4(x+2)(y+1)=0 ⇒5x^2 +8y^2 +4xy−36=0 step 3: find the major and minor axis express the eqn. in polar form with x=r cos θ, y=r sin θ 5r^2 cos^2 θ+8r^2 sin^2 θ+4r^2 sin θcos θ−36=0 [(5/2)(cos 2θ+1)+4(1−cos 2θ)+2sin 2θ]r^2 −36=0 (13−3cos 2θ+4sin 2θ)r^2 =72 [13+5(−(3/5)cos 2θ+(4/5)sin 2θ)]r^2 =72 [13+5(−sin αcos 2θ+cos αsin 2θ)]r^2 =72 [13+5 sin (2θ−α)]r^2 =72 ⇒r=((6(√2))/( (√(13+5 sin (2θ−α))))) r_(max) =major axis=a=((6(√2))/( (√(13−5))))=3 at 2θ−α=−(π/2) or θ=tan^(−1) (1/3)−(π/4) r_(min) =minor axis=b=((6(√2))/( (√(13+5))))=2 at 2θ−α=(π/2) or θ=tan^(−1) (1/3)+(π/4) we know in this way also that the ellipse is rotated by angle tan^(−1) (1/3)−(π/4)](https://www.tinkutara.com/question/Q78228.png)
$${if}\:{you}\:{don}'{t}\:{like}\:{to}\:{learn}\:{too}\:{many} \\ $$$${formulas},\:{you}\:{can}\:{determine}\:{the} \\ $$$${parameters}\:{of}\:{the}\:{ellipse}\:{in}\:{following} \\ $$$${way}: \\ $$$$ \\ $$$${step}\:\mathrm{1}:\:{determine}\:{center}\:{point} \\ $$$${that}\:{means}\:{to}\:{determine}\:{the}\:{range}\:{of} \\ $$$${x}\:{and}\:{y}\:{ordinates}.\:\left({see}\:{also}\:{sir}\:{MJS}'\:{post}\right) \\ $$$${we}\:{form}\:{eqn}.\:{as}\:{quadratic}\:{eqn}.\:{w}.{r}.{t}.\:{y}: \\ $$$$\mathrm{8}{y}^{\mathrm{2}} +\mathrm{4}\left({x}−\mathrm{6}\right){y}+\mathrm{5}{x}^{\mathrm{2}} −\mathrm{24}{x}=\mathrm{0} \\ $$$$\Delta=\mathrm{4}^{\mathrm{2}} \left({x}−\mathrm{6}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{8}×\left(\mathrm{5}{x}^{\mathrm{2}} −\mathrm{24}{x}\right)\geqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{6}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{5}{x}^{\mathrm{2}} −\mathrm{24}{x}\right)\geqslant\mathrm{0} \\ $$$$−{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}\geqslant\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{4}\leqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{8}\leqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}\leqslant{x}\leqslant\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{x}_{{C}} =\mathrm{2} \\ $$$${we}\:{form}\:{eqn}.\:{as}\:{quadratic}\:{eqn}.\:{w}.{r}.{t}.\:{x}: \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}\left({y}−\mathrm{6}\right){x}+\mathrm{8}{y}^{\mathrm{2}} −\mathrm{24}{y}=\mathrm{0} \\ $$$$\Delta=\mathrm{4}^{\mathrm{2}} \left({y}−\mathrm{6}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{5}\left(\mathrm{8}{y}^{\mathrm{2}} −\mathrm{24}{y}\right)\geqslant\mathrm{0} \\ $$$$\left({y}−\mathrm{6}\right)^{\mathrm{2}} −\mathrm{5}\left(\mathrm{2}{y}^{\mathrm{2}} −\mathrm{6}{y}\right)\geqslant\mathrm{0} \\ $$$$−{y}^{\mathrm{2}} +\mathrm{2}{y}+\mathrm{4}\geqslant\mathrm{0} \\ $$$${y}^{\mathrm{2}} −\mathrm{2}{y}−\mathrm{4}\leqslant\mathrm{0} \\ $$$$\left({y}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{5}\leqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}−\sqrt{\mathrm{5}}\leqslant{y}\leqslant\mathrm{1}+\sqrt{\mathrm{5}} \\ $$$$\Rightarrow{y}_{{C}} =\mathrm{1} \\ $$$$\Rightarrow{center}\:{point}\:{of}\:{ellipse}\:{is}\:{C}\left(\mathrm{2},\mathrm{1}\right) \\ $$$$ \\ $$$${step}\:\mathrm{2}:\:{make}\:{the}\:{center}\:{point}\:{as}\:{origin} \\ $$$${replace}\:{x}\:{with}\:{x}+{x}_{{C}} \:{and}\:{y}\:{with}\:{y}+{y}_{{C}} \\ $$$${in}\:{the}\:{eqn}. \\ $$$$\mathrm{5}\left({x}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{8}\left({y}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{24}\left({x}+\mathrm{2}\right)−\mathrm{24}\left({y}+\mathrm{1}\right)+\mathrm{4}\left({x}+\mathrm{2}\right)\left({y}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{5}{x}^{\mathrm{2}} +\mathrm{8}{y}^{\mathrm{2}} +\mathrm{4}{xy}−\mathrm{36}=\mathrm{0} \\ $$$$ \\ $$$${step}\:\mathrm{3}:\:{find}\:{the}\:{major}\:{and}\:{minor}\:{axis} \\ $$$${express}\:{the}\:{eqn}.\:{in}\:{polar}\:{form}\:{with} \\ $$$${x}={r}\:\mathrm{cos}\:\theta,\:{y}={r}\:\mathrm{sin}\:\theta \\ $$$$\mathrm{5}{r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{8}{r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{4}{r}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta−\mathrm{36}=\mathrm{0} \\ $$$$\left[\frac{\mathrm{5}}{\mathrm{2}}\left(\mathrm{cos}\:\mathrm{2}\theta+\mathrm{1}\right)+\mathrm{4}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right)+\mathrm{2sin}\:\mathrm{2}\theta\right]{r}^{\mathrm{2}} −\mathrm{36}=\mathrm{0} \\ $$$$\left(\mathrm{13}−\mathrm{3cos}\:\mathrm{2}\theta+\mathrm{4sin}\:\mathrm{2}\theta\right){r}^{\mathrm{2}} =\mathrm{72} \\ $$$$\left[\mathrm{13}+\mathrm{5}\left(−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{cos}\:\mathrm{2}\theta+\frac{\mathrm{4}}{\mathrm{5}}\mathrm{sin}\:\mathrm{2}\theta\right)\right]{r}^{\mathrm{2}} =\mathrm{72} \\ $$$$\left[\mathrm{13}+\mathrm{5}\left(−\mathrm{sin}\:\alpha\mathrm{cos}\:\mathrm{2}\theta+\mathrm{cos}\:\alpha\mathrm{sin}\:\mathrm{2}\theta\right)\right]{r}^{\mathrm{2}} =\mathrm{72} \\ $$$$\left[\mathrm{13}+\mathrm{5}\:\mathrm{sin}\:\left(\mathrm{2}\theta−\alpha\right)\right]{r}^{\mathrm{2}} =\mathrm{72} \\ $$$$\Rightarrow{r}=\frac{\mathrm{6}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{13}+\mathrm{5}\:\mathrm{sin}\:\left(\mathrm{2}\theta−\alpha\right)}} \\ $$$${r}_{{max}} ={major}\:{axis}={a}=\frac{\mathrm{6}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{13}−\mathrm{5}}}=\mathrm{3} \\ $$$${at}\:\mathrm{2}\theta−\alpha=−\frac{\pi}{\mathrm{2}}\:{or}\:\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}−\frac{\pi}{\mathrm{4}} \\ $$$${r}_{{min}} ={minor}\:{axis}={b}=\frac{\mathrm{6}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{13}+\mathrm{5}}}=\mathrm{2} \\ $$$${at}\:\mathrm{2}\theta−\alpha=\frac{\pi}{\mathrm{2}}\:{or}\:\theta=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}+\frac{\pi}{\mathrm{4}} \\ $$$${we}\:{know}\:{in}\:{this}\:{way}\:{also}\:{that}\:{the} \\ $$$${ellipse}\:{is}\:{rotated}\:{by}\:{angle}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}−\frac{\pi}{\mathrm{4}} \\ $$
Commented by mr W last updated on 15/Jan/20

