Question Number 8168 by aungnaingsoe last updated on 02/Oct/16
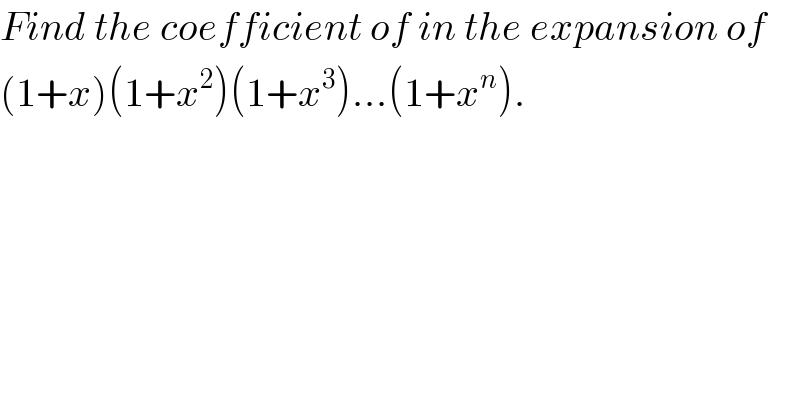
$${Find}\:{the}\:{coefficient}\:{of}\:{in}\:{the}\:{expansion}\:{of} \\ $$$$\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{3}} \right)…\left(\mathrm{1}+{x}^{{n}} \right). \\ $$
Commented by Rasheed Soomro last updated on 02/Oct/16
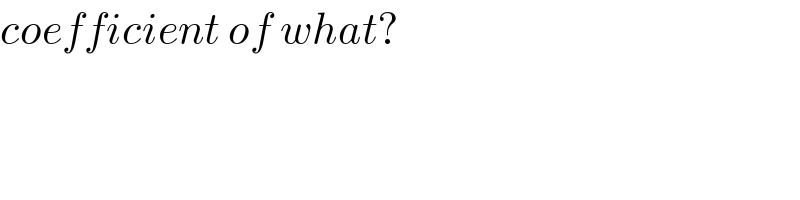
$${coefficient}\:{of}\:{what}? \\ $$
Commented by lepan last updated on 02/Oct/16

$${x}^{\mathrm{9}} \\ $$
Commented by 123456 last updated on 03/Oct/16
![[(0),(1) ] [(0),(2) ] [(0),(3) ]... [(0),(n) ] p_n (x)=Π_(i=1) ^n (1+x^i ) 1≤n≤3 G[p_n ]≤6⇒C_9 =0 n≥4 G[p_n ]≥9 −−−−−−−−−−− 2 18,27,36,45:4 3 •1 126,135:2 •2 234:1 −−−−−−−−− n=4⇒C_9 =1 n=5⇒C_9 =3 n=6⇒C_9 =5 n=7⇒C_9 =6 n≥8⇒C_9 =7](https://www.tinkutara.com/question/Q8223.png)
$$\begin{bmatrix}{\mathrm{0}}\\{\mathrm{1}}\end{bmatrix}\begin{bmatrix}{\mathrm{0}}\\{\mathrm{2}}\end{bmatrix}\begin{bmatrix}{\mathrm{0}}\\{\mathrm{3}}\end{bmatrix}…\begin{bmatrix}{\mathrm{0}}\\{{n}}\end{bmatrix} \\ $$$${p}_{{n}} \left({x}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}+{x}^{{i}} \right) \\ $$$$\mathrm{1}\leqslant{n}\leqslant\mathrm{3} \\ $$$$\mathrm{G}\left[{p}_{{n}} \right]\leqslant\mathrm{6}\Rightarrow{C}_{\mathrm{9}} =\mathrm{0} \\ $$$${n}\geqslant\mathrm{4} \\ $$$$\mathrm{G}\left[{p}_{{n}} \right]\geqslant\mathrm{9} \\ $$$$−−−−−−−−−−− \\ $$$$\mathrm{2} \\ $$$$\mathrm{18},\mathrm{27},\mathrm{36},\mathrm{45}:\mathrm{4} \\ $$$$\mathrm{3} \\ $$$$\bullet\mathrm{1} \\ $$$$\mathrm{126},\mathrm{135}:\mathrm{2} \\ $$$$\bullet\mathrm{2} \\ $$$$\mathrm{234}:\mathrm{1} \\ $$$$−−−−−−−−− \\ $$$${n}=\mathrm{4}\Rightarrow{C}_{\mathrm{9}} =\mathrm{1} \\ $$$${n}=\mathrm{5}\Rightarrow{C}_{\mathrm{9}} =\mathrm{3} \\ $$$${n}=\mathrm{6}\Rightarrow{C}_{\mathrm{9}} =\mathrm{5} \\ $$$${n}=\mathrm{7}\Rightarrow{C}_{\mathrm{9}} =\mathrm{6} \\ $$$${n}\geqslant\mathrm{8}\Rightarrow{C}_{\mathrm{9}} =\mathrm{7} \\ $$
