Question Number 9747 by tawakalitu last updated on 30/Dec/16
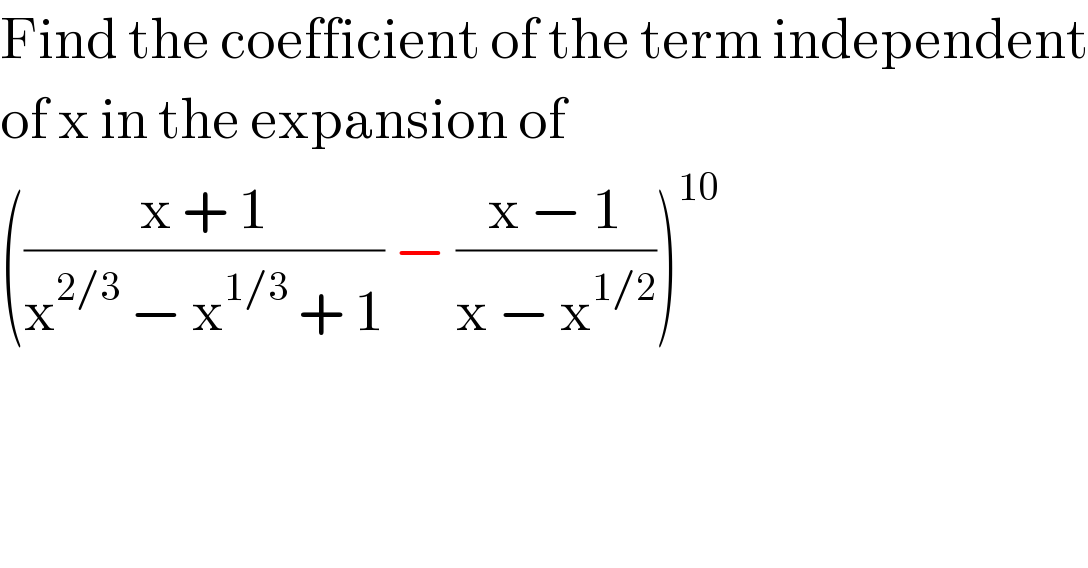
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:\mathrm{the}\:\mathrm{term}\:\mathrm{independent} \\ $$$$\mathrm{of}\:\mathrm{x}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of} \\ $$$$\left(\frac{\mathrm{x}\:+\:\mathrm{1}}{\mathrm{x}^{\mathrm{2}/\mathrm{3}} \:−\:\mathrm{x}^{\mathrm{1}/\mathrm{3}} \:+\:\mathrm{1}}\:−\:\frac{\mathrm{x}\:−\:\mathrm{1}}{\mathrm{x}\:−\:\mathrm{x}^{\mathrm{1}/\mathrm{2}} }\right)^{\mathrm{10}} \\ $$
Answered by sandy_suhendra last updated on 30/Dec/16
![using the formula : a^3 +b^3 =(a+b)(a^2 −ab+b^2 ) a^2 −b^2 =(a+b)(a−b) [(((x^(1/3) )^3 +1^3 )/(x^(2/3) −x^(1/3) +1)) − (((x^(1/2) )^2 −1^2 )/(x^(1/2) (x^(1/2) −1)))]^(10) =[(((x^(1/3) +1)(x^(2/3) −x^(1/3) +1))/(x^(2/3) −x^(1/3) +1)) − (((x^(1/2) +1)(x^(1/2) −1))/(x^(1/2) (x^(1/2) −1)))]^(10) =[x^(1/3) +1−1−(1/x^(1/2) )]^(10) =[x^(1/3) −(1/x^(1/2) )]^(10) the term independent of x = x^0 ⇒ 10C6 (x^(1/3) )^6 (−(1/x^(1/2) ))^4 = 210 x^0 so the coefficient is 210](https://www.tinkutara.com/question/Q9749.png)
$$\mathrm{using}\:\mathrm{the}\:\mathrm{formula}\:: \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} =\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{ab}+\mathrm{b}^{\mathrm{2}} \right) \\ $$$$\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} =\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}−\mathrm{b}\right) \\ $$$$ \\ $$$$\left[\frac{\left(\mathrm{x}^{\mathrm{1}/\mathrm{3}} \right)^{\mathrm{3}} +\mathrm{1}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{2}/\mathrm{3}} −\mathrm{x}^{\mathrm{1}/\mathrm{3}} +\mathrm{1}}\:−\:\frac{\left(\mathrm{x}^{\mathrm{1}/\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{1}/\mathrm{2}} \left(\mathrm{x}^{\mathrm{1}/\mathrm{2}} −\mathrm{1}\right)}\right]^{\mathrm{10}} \\ $$$$=\left[\frac{\left(\mathrm{x}^{\mathrm{1}/\mathrm{3}} +\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}/\mathrm{3}} −\mathrm{x}^{\mathrm{1}/\mathrm{3}} +\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}/\mathrm{3}} −\mathrm{x}^{\mathrm{1}/\mathrm{3}} +\mathrm{1}}\:−\:\frac{\left(\mathrm{x}^{\mathrm{1}/\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{1}/\mathrm{2}} −\mathrm{1}\right)}{\mathrm{x}^{\mathrm{1}/\mathrm{2}} \left(\mathrm{x}^{\mathrm{1}/\mathrm{2}} −\mathrm{1}\right)}\right]^{\mathrm{10}} \\ $$$$=\left[\mathrm{x}^{\mathrm{1}/\mathrm{3}} +\mathrm{1}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }\right]^{\mathrm{10}} \\ $$$$=\left[\mathrm{x}^{\mathrm{1}/\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }\right]^{\mathrm{10}} \\ $$$$\mathrm{the}\:\mathrm{term}\:\mathrm{independent}\:\mathrm{of}\:\mathrm{x}\:=\:\mathrm{x}^{\mathrm{0}} \\ $$$$\Rightarrow\:\mathrm{10C6}\:\left(\mathrm{x}^{\mathrm{1}/\mathrm{3}} \right)^{\mathrm{6}} \left(−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{1}/\mathrm{2}} }\right)^{\mathrm{4}} \:=\:\mathrm{210}\:\mathrm{x}^{\mathrm{0}} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{is}\:\mathrm{210} \\ $$$$ \\ $$
Commented by tawakalitu last updated on 30/Dec/16
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
