find-the-constant-a-b-and-c-so-that-the-direction-derivative-of-axy-2-byz-cz-2-x-3-at-1-2-1-has-a-maximum-of-magnitude-64-jn-a-direction-parallel-to-the-z-axis-

Question Number 65797 by Souvik Ghosh last updated on 04/Aug/19

f i n d t h e c o n s t a n t a, b a n d c s o

t h a t t h e d i r e c t i o n d e r i v a t i v e o f

Φ = {a x y}^{2} + b y z + {c z}^{2} x^{3} a t (1, 2, - 1)

h a s a m a x i m u m o f m a g n i t u d e

64 j n a d i r e c t i o n p a r a l l e l t o t h e

z a x i s .

Answered by Tanmay chaudhury last updated on 04/Aug/19

▽ Φ

(i \frac{\partial}{\partial x} + j \frac{\partial}{\partial y} + k \frac{\partial}{\partial z}) ({a x y}^{2} + b y z + {c z}^{2} x^{3})

i ({a y}^{2} + 3 x^{2} {c z}^{2}) + j (2 a x y + b z) + k (b y + 2 {c x}^{3} z)

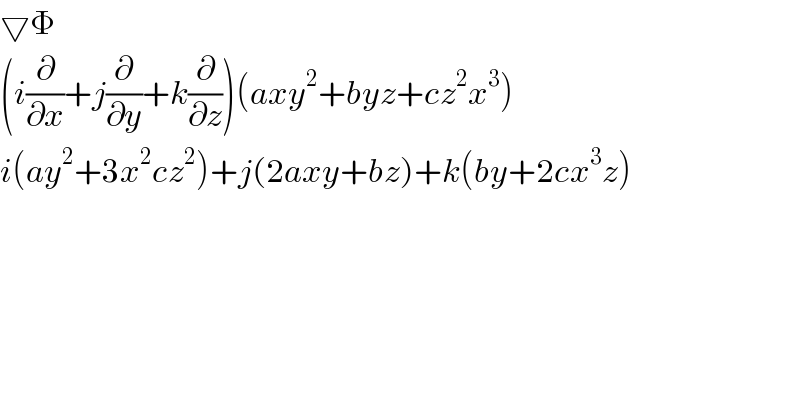
Commented by Tanmay chaudhury last updated on 04/Aug/19

e a i t i h a v e c o r r e c t e d m y e r r o r d e t e c t e d b y y o u . . t h a n k y o u

w a i t i a m t r y i n g

Commented by Souvik Ghosh last updated on 04/Aug/19

b u t s i r h e a r

\vec{▽} Φ = ({a y}^{2} + 3 {c z}^{2} x^{2}) i + (2 a x y + b z) j

+ (b y + 2 {c z x}^{3}) k

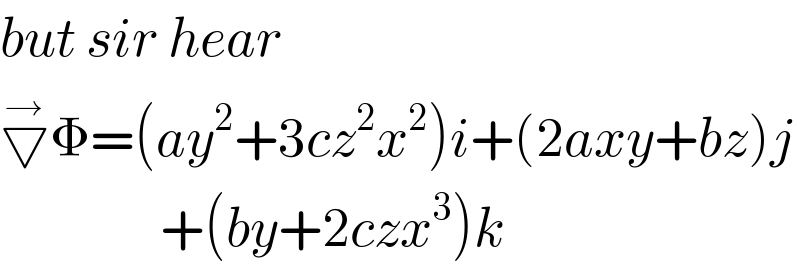
Commented by Tanmay chaudhury last updated on 04/Aug/19

y e s y o u a r e r i g h t \dots i n h u r r y