Question Number 70030 by Joel122 last updated on 30/Sep/19
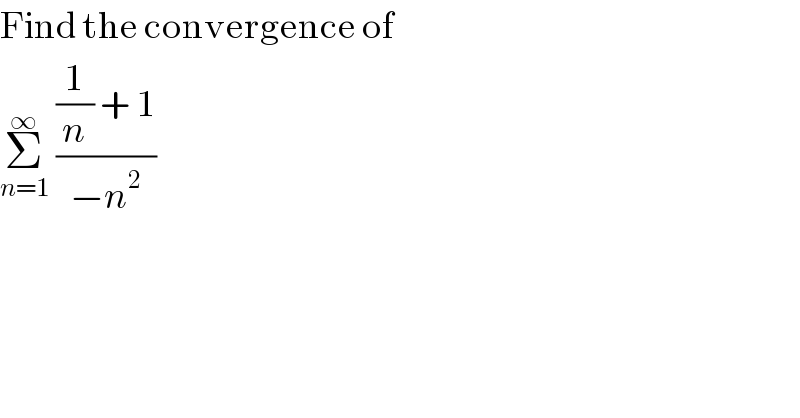
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{convergence}\:\mathrm{of} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\frac{\mathrm{1}}{{n}}\:+\:\mathrm{1}}{−{n}^{\mathrm{2}} } \\ $$
Answered by mind is power last updated on 30/Sep/19
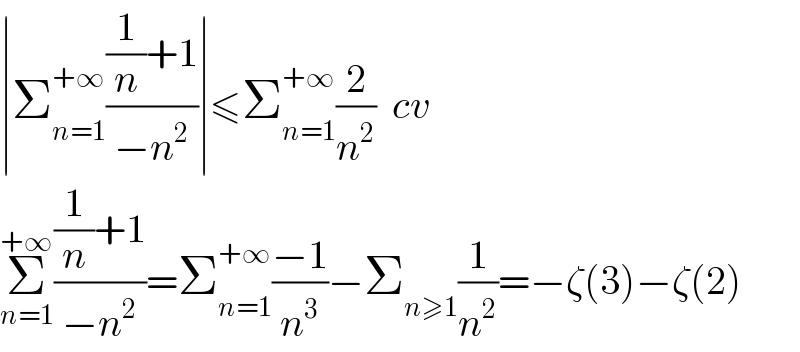
$$\mid\sum_{{n}=\mathrm{1}} ^{+\infty} \frac{\frac{\mathrm{1}}{{n}}+\mathrm{1}}{−{n}^{\mathrm{2}} }\mid\leqslant\sum_{{n}=\mathrm{1}} ^{+\infty} \frac{\mathrm{2}}{{n}^{\mathrm{2}} }\:\:{cv}\: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\frac{\mathrm{1}}{{n}}+\mathrm{1}}{−{n}^{\mathrm{2}} }=\sum_{{n}=\mathrm{1}} ^{+\infty} \frac{−\mathrm{1}}{{n}^{\mathrm{3}} }−\sum_{{n}\geqslant\mathrm{1}} \frac{\mathrm{1}}{{n}^{\mathrm{2}} }=−\zeta\left(\mathrm{3}\right)−\zeta\left(\mathrm{2}\right) \\ $$
