Question Number 131775 by Raxreedoroid last updated on 08/Feb/21
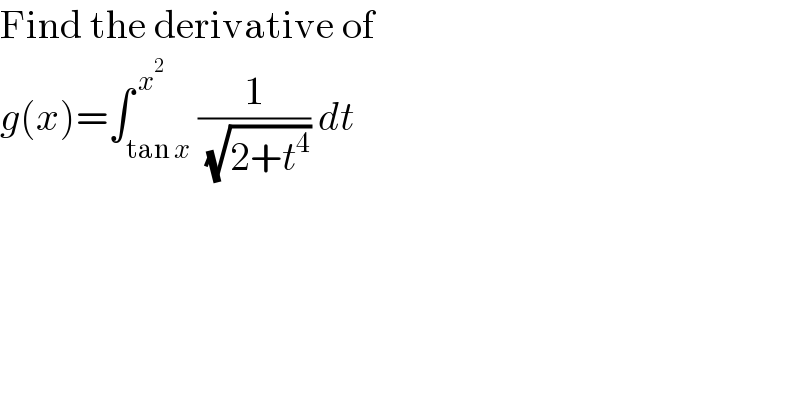
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{derivative}\:\mathrm{of} \\ $$$${g}\left({x}\right)=\int_{\mathrm{tan}\:{x}} ^{\:{x}^{\mathrm{2}} } \frac{\mathrm{1}}{\:\sqrt{\mathrm{2}+{t}^{\mathrm{4}} }}\:{dt} \\ $$
Answered by bemath last updated on 08/Feb/21
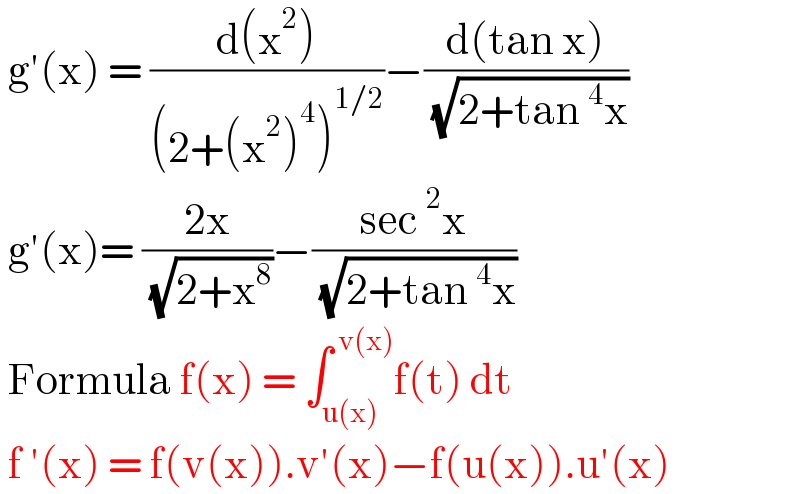
$$\:\mathrm{g}'\left(\mathrm{x}\right)\:=\:\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{2}+\left(\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{4}} \right)^{\mathrm{1}/\mathrm{2}} }−\frac{\mathrm{d}\left(\mathrm{tan}\:\mathrm{x}\right)}{\:\sqrt{\mathrm{2}+\mathrm{tan}\:^{\mathrm{4}} \mathrm{x}}} \\ $$$$\:\mathrm{g}'\left(\mathrm{x}\right)=\:\frac{\mathrm{2x}}{\:\sqrt{\mathrm{2}+\mathrm{x}^{\mathrm{8}} }}−\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\:\sqrt{\mathrm{2}+\mathrm{tan}\:^{\mathrm{4}} \mathrm{x}}}\: \\ $$$$\:\mathrm{Formula}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\int_{\mathrm{u}\left(\mathrm{x}\right)} ^{\:\mathrm{v}\left(\mathrm{x}\right)} \mathrm{f}\left(\mathrm{t}\right)\:\mathrm{dt}\: \\ $$$$\:\mathrm{f}\:'\left(\mathrm{x}\right)\:=\:\mathrm{f}\left(\mathrm{v}\left(\mathrm{x}\right)\right).\mathrm{v}'\left(\mathrm{x}\right)−\mathrm{f}\left(\mathrm{u}\left(\mathrm{x}\right)\right).\mathrm{u}'\left(\mathrm{x}\right) \\ $$
Commented by Raxreedoroid last updated on 08/Feb/21

$${Thanks}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 08/Feb/21
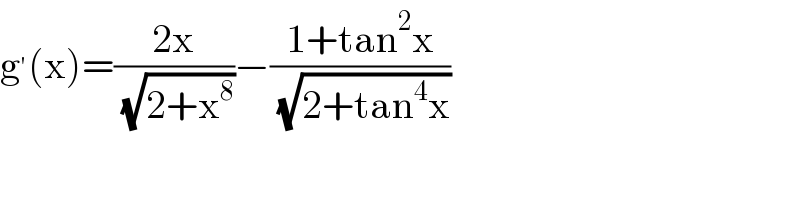
$$\mathrm{g}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{2x}}{\:\sqrt{\mathrm{2}+\mathrm{x}^{\mathrm{8}} }}−\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\:\sqrt{\mathrm{2}+\mathrm{tan}^{\mathrm{4}} \mathrm{x}}} \\ $$
Commented by Raxreedoroid last updated on 08/Feb/21
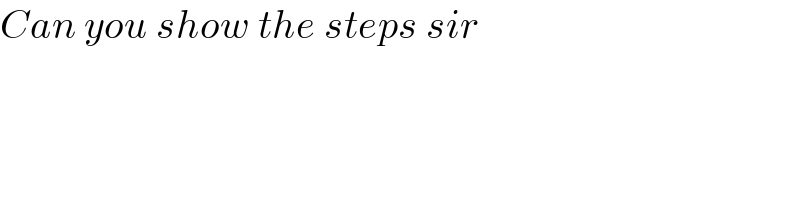
$${Can}\:{you}\:{show}\:{the}\:{steps}\:{sir} \\ $$
