Question Number 1012 by rpatle69@gmail.com last updated on 13/May/15

$${find}\:{the}\:{equation}\:{of}\:{circle}\:{whose} \\ $$$${parametric}\:{form}\:{is}\:{given}\:{by}\: \\ $$$${x}=\mathrm{3cos}\:\theta+\mathrm{5}\:{and}\:{y}=\:\mathrm{3sin}\:\theta−\mathrm{7}\:{and} \\ $$$${second}\:{part}\:{is}\:{x}=\mathrm{4cos}\:\theta−\mathrm{3}\:{and} \\ $$$${y}=\mathrm{4sin}\:\theta+\mathrm{4}.\:{find}\:{centre}\:{and}\: \\ $$$${radius}\:{of}\:{above}\:{circle}. \\ $$$$ \\ $$$$ \\ $$$${guys}\:{plz}\:{ans}.\:{me}\:{soon}….. \\ $$$$ \\ $$
Answered by sudhanshur last updated on 13/May/15

$${x}−\mathrm{5}=\mathrm{3cos}\:\theta \\ $$$${y}+\mathrm{7}=\mathrm{3sin}\:\theta \\ $$$${square}\:{and}\:{add} \\ $$$$\left({x}−\mathrm{5}\right)^{\mathrm{2}} +\left({y}+\mathrm{7}\right)^{\mathrm{2}} =\mathrm{9} \\ $$
Answered by sudhanshur last updated on 13/May/15
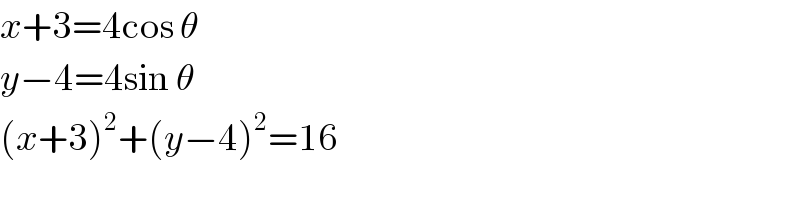
$${x}+\mathrm{3}=\mathrm{4cos}\:\theta \\ $$$${y}−\mathrm{4}=\mathrm{4sin}\:\theta \\ $$$$\left({x}+\mathrm{3}\right)^{\mathrm{2}} +\left({y}−\mathrm{4}\right)^{\mathrm{2}} =\mathrm{16} \\ $$
