Find-the-equation-of-the-circle-having-2-2-as-its-centre-and-passing-through-3x-y-14-2x-5y-18-

Question Number 76860 by vishalbhardwaj last updated on 31/Dec/19

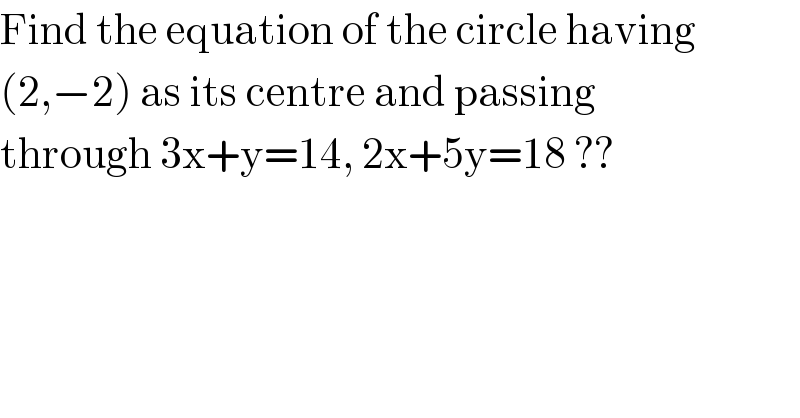
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{having} \\ $$$$\left(\mathrm{2},−\mathrm{2}\right)\:\mathrm{as}\:\mathrm{its}\:\mathrm{centre}\:\mathrm{and}\:\mathrm{passing} \\ $$$$\mathrm{through}\:\mathrm{3x}+\mathrm{y}=\mathrm{14},\:\mathrm{2x}+\mathrm{5y}=\mathrm{18}\:?? \\ $$

Answered by john santu last updated on 31/Dec/19

r = (√( (4−2)^2 +(2+2)^2 )) r = (√(20)) circle (x−2)^2 +(y+2)^2 =20.

$${r}\:=\:\sqrt{\:\left(\mathrm{4}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{2}+\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${r}\:=\:\sqrt{\mathrm{20}}\: \\ $$$${circle}\:\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{20}.\: \\ $$

Commented by vishalbhardwaj last updated on 31/Dec/19

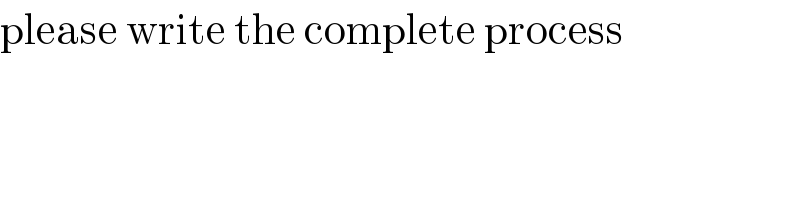
$$\mathrm{please}\:\mathrm{write}\:\mathrm{the}\:\mathrm{complete}\:\mathrm{process} \\ $$

Commented by vishalbhardwaj last updated on 31/Dec/19

sir it is not given that thd circle will pass through intersecting point of lines.....

$$\mathrm{sir}\:\mathrm{it}\:\mathrm{is}\:\mathrm{not}\:\mathrm{given}\:\mathrm{that}\:\mathrm{thd}\:\mathrm{circle} \\ $$$$\mathrm{will}\:\mathrm{pass}\:\mathrm{through}\:\mathrm{intersecting} \\ $$$$\mathrm{point}\:\mathrm{of}\:\mathrm{lines}….. \\ $$

Commented by jagoll last updated on 31/Dec/19

Commented by jagoll last updated on 31/Dec/19

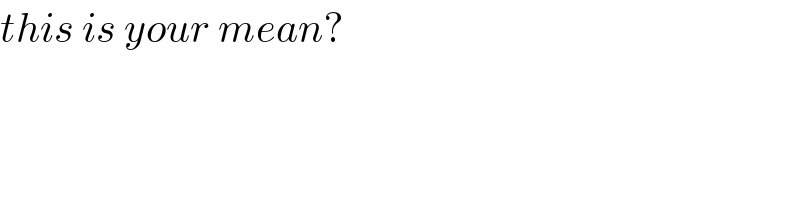
$${this}\:{is}\:{your}\:{mean}? \\ $$

Commented by MJS last updated on 31/Dec/19

if the circle doesn′t pass through the intersection of the lines, what else could it mean?

$$\mathrm{if}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{pass}\:\mathrm{through}\:\mathrm{the} \\ $$$$\mathrm{intersection}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lines},\:\mathrm{what}\:\mathrm{else}\:\mathrm{could}\:\mathrm{it} \\ $$$$\mathrm{mean}? \\ $$

Commented by MJS last updated on 31/Dec/19

the lines cannot be tangents because the distances to the given center are different ((√(10)) & ((24(√(29)))/(29)))

$$\mathrm{the}\:\mathrm{lines}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{tangents}\:\mathrm{because}\:\mathrm{the} \\ $$$$\mathrm{distances}\:\mathrm{to}\:\mathrm{the}\:\mathrm{given}\:\mathrm{center}\:\mathrm{are}\:\mathrm{different} \\ $$$$\left(\sqrt{\mathrm{10}}\:\&\:\frac{\mathrm{24}\sqrt{\mathrm{29}}}{\mathrm{29}}\right) \\ $$

Answered by MJS last updated on 31/Dec/19

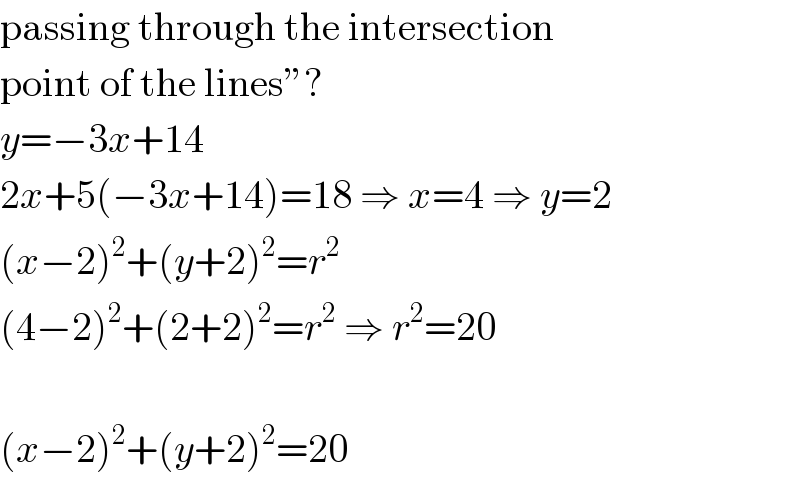
passing through the intersection point of the lines”? y=−3x+14 2x+5(−3x+14)=18 ⇒ x=4 ⇒ y=2 (x−2)^2 +(y+2)^2 =r^2 (4−2)^2 +(2+2)^2 =r^2 ⇒ r^2 =20 (x−2)^2 +(y+2)^2 =20

$$\mathrm{passing}\:\mathrm{through}\:\mathrm{the}\:\mathrm{intersection} \\ $$$$\mathrm{point}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lines}''? \\ $$$${y}=−\mathrm{3}{x}+\mathrm{14} \\ $$$$\mathrm{2}{x}+\mathrm{5}\left(−\mathrm{3}{x}+\mathrm{14}\right)=\mathrm{18}\:\Rightarrow\:{x}=\mathrm{4}\:\Rightarrow\:{y}=\mathrm{2} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\mathrm{4}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{2}+\mathrm{2}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\Rightarrow\:{r}^{\mathrm{2}} =\mathrm{20} \\ $$$$ \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} =\mathrm{20} \\ $$

Facebook Tweet Pin

Find-the-equation-of-the-circle-having-2-2-as-its-centre-and-passing-through-3x-y-14-2x-5y-18-

Leave a Reply Cancel reply