Question Number 135000 by bobhans last updated on 09/Mar/21

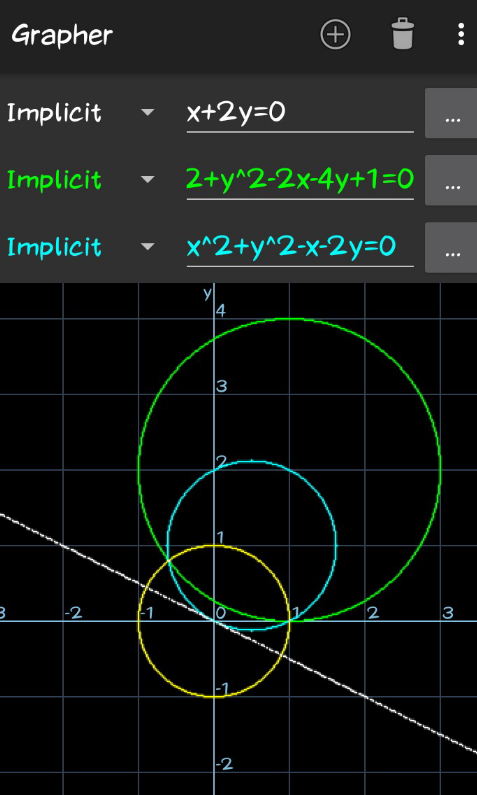
$$ \\ $$Find the equation of the circle through the points of intersection of x^2+y^2−1=0,x^2+y^2−2x−4y+1=0 and touching the line x+2y=0?
Answered by EDWIN88 last updated on 09/Mar/21
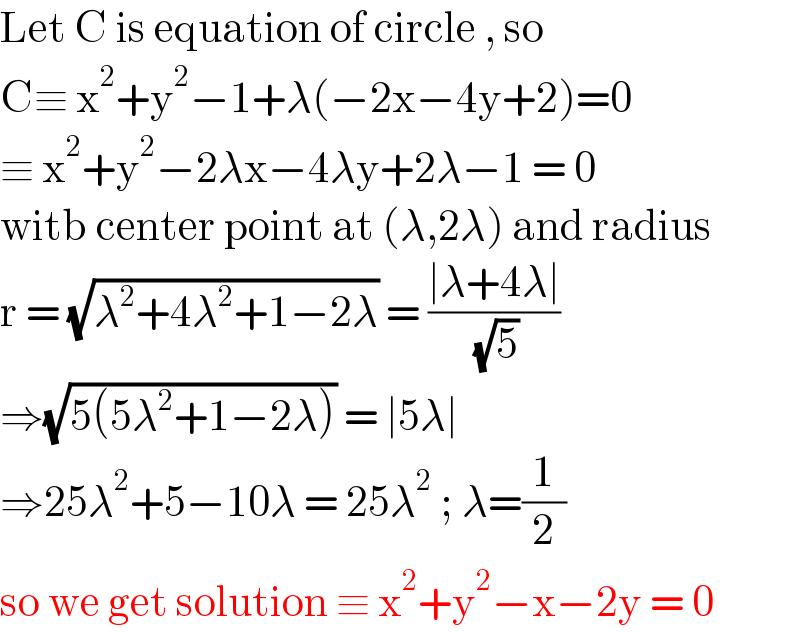
$$\mathrm{Let}\:\mathrm{C}\:\mathrm{is}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{circle}\:,\:\mathrm{so}\: \\ $$$$\mathrm{C}\equiv\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{1}+\lambda\left(−\mathrm{2x}−\mathrm{4y}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\equiv\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2}\lambda\mathrm{x}−\mathrm{4}\lambda\mathrm{y}+\mathrm{2}\lambda−\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{witb}\:\mathrm{center}\:\mathrm{point}\:\mathrm{at}\:\left(\lambda,\mathrm{2}\lambda\right)\:\mathrm{and}\:\mathrm{radius}\: \\ $$$$\mathrm{r}\:=\:\sqrt{\lambda^{\mathrm{2}} +\mathrm{4}\lambda^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\lambda}\:=\:\frac{\mid\lambda+\mathrm{4}\lambda\mid}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow\sqrt{\mathrm{5}\left(\mathrm{5}\lambda^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\lambda\right)}\:=\:\mid\mathrm{5}\lambda\mid \\ $$$$\Rightarrow\mathrm{25}\lambda^{\mathrm{2}} +\mathrm{5}−\mathrm{10}\lambda\:=\:\mathrm{25}\lambda^{\mathrm{2}} \:;\:\lambda=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{get}\:\mathrm{solution}\:\equiv\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{x}−\mathrm{2y}\:=\:\mathrm{0} \\ $$
Commented by bobhans last updated on 09/Mar/21