Find-the-equation-of-the-circle-which-is-orthogonal-to-the-circles-x-2-y-2-7x-y-0-and-x-2-y-2-3x-6y-5-0-and-which-passes-through-the-point-3-0-

Question Number 142208 by ZiYangLee last updated on 27/May/21

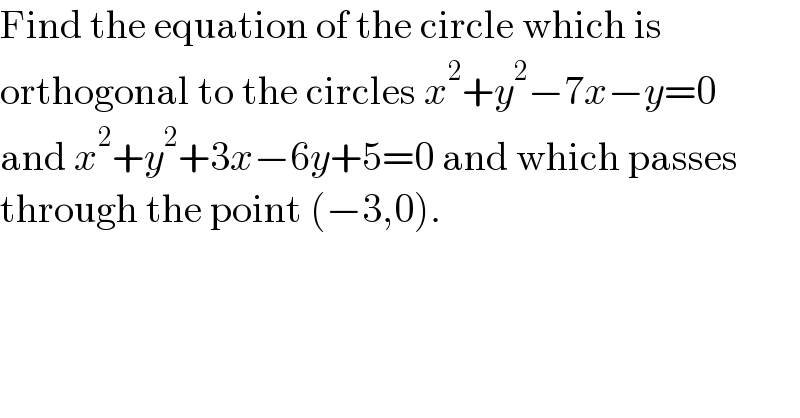
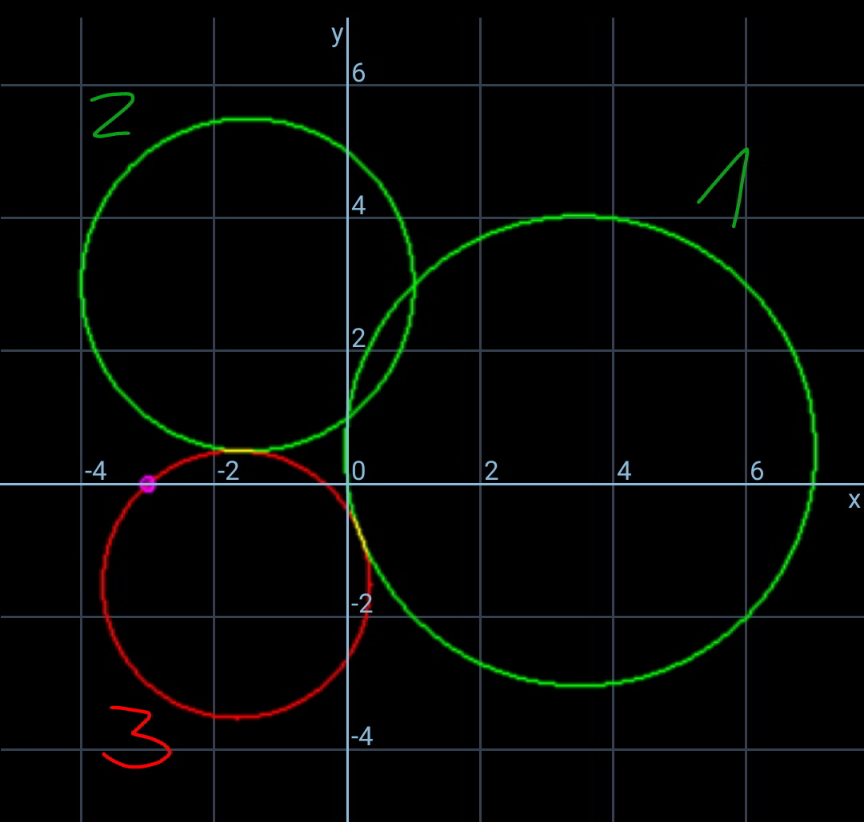
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{which}\:\mathrm{is} \\ $$$$\mathrm{orthogonal}\:\mathrm{to}\:\mathrm{the}\:\mathrm{circles}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{7}{x}−{y}=\mathrm{0} \\ $$$$\mathrm{and}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{6}{y}+\mathrm{5}=\mathrm{0}\:\mathrm{and}\:\mathrm{which}\:\mathrm{passes} \\ $$$$\mathrm{through}\:\mathrm{the}\:\mathrm{point}\:\left(−\mathrm{3},\mathrm{0}\right). \\ $$

Answered by mr W last updated on 27/May/21

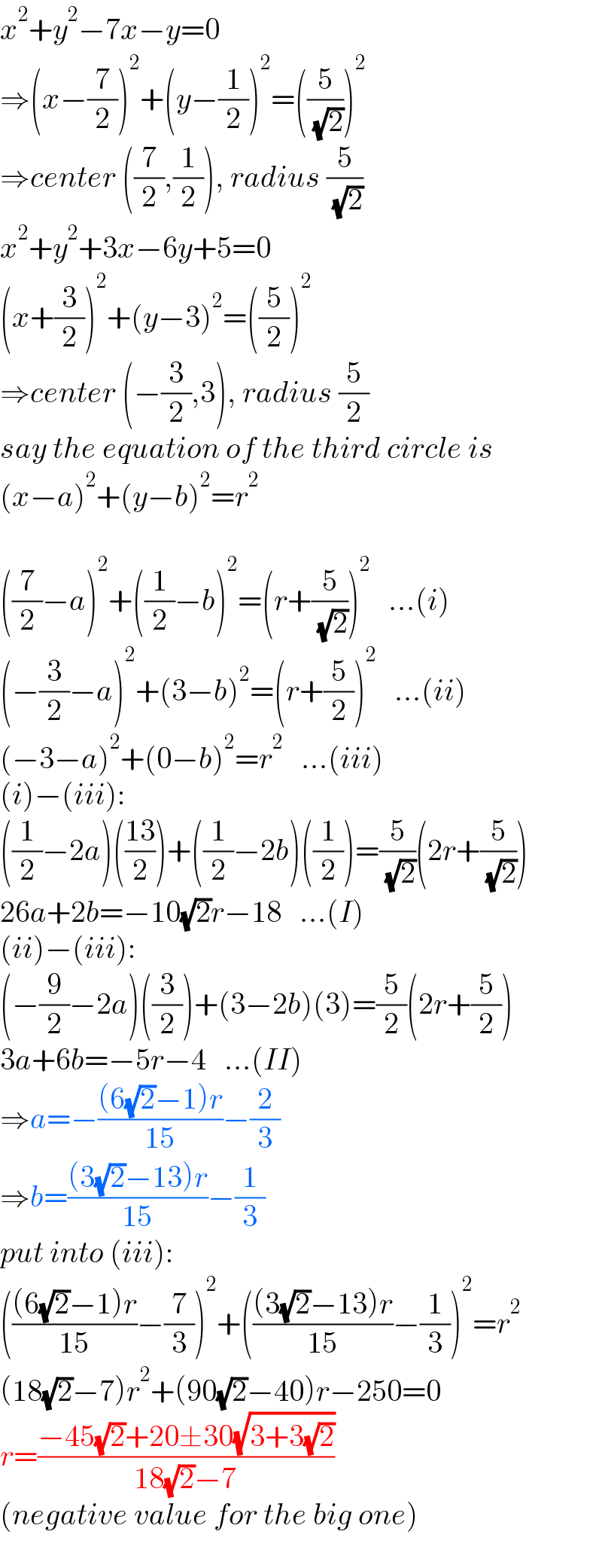
x^2 +y^2 −7x−y=0 ⇒(x−(7/2))^2 +(y−(1/2))^2 =((5/( (√2))))^2 ⇒center ((7/2),(1/2)), radius (5/( (√2))) x^2 +y^2 +3x−6y+5=0 (x+(3/2))^2 +(y−3)^2 =((5/2))^2 ⇒center (−(3/2),3), radius (5/2) say the equation of the third circle is (x−a)^2 +(y−b)^2 =r^2 ((7/2)−a)^2 +((1/2)−b)^2 =(r+(5/( (√2))))^2 ...(i) (−(3/2)−a)^2 +(3−b)^2 =(r+(5/2))^2 ...(ii) (−3−a)^2 +(0−b)^2 =r^2 ...(iii) (i)−(iii): ((1/2)−2a)(((13)/2))+((1/2)−2b)((1/2))=(5/( (√2)))(2r+(5/( (√2)))) 26a+2b=−10(√2)r−18 ...(I) (ii)−(iii): (−(9/2)−2a)((3/2))+(3−2b)(3)=(5/2)(2r+(5/2)) 3a+6b=−5r−4 ...(II) ⇒a=−(((6(√2)−1)r)/(15))−(2/3) ⇒b=(((3(√2)−13)r)/(15))−(1/3) put into (iii): ((((6(√2)−1)r)/(15))−(7/3))^2 +((((3(√2)−13)r)/(15))−(1/3))^2 =r^2 (18(√2)−7)r^2 +(90(√2)−40)r−250=0 r=((−45(√2)+20±30(√(3+3(√2))))/(18(√2)−7)) (negative value for the big one)

$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{7}{x}−{y}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{5}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{center}\:\left(\frac{\mathrm{7}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right),\:{radius}\:\frac{\mathrm{5}}{\:\sqrt{\mathrm{2}}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{6}{y}+\mathrm{5}=\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} =\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{center}\:\left(−\frac{\mathrm{3}}{\mathrm{2}},\mathrm{3}\right),\:{radius}\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${say}\:{the}\:{equation}\:{of}\:{the}\:{third}\:{circle}\:{is} \\ $$$$\left({x}−{a}\right)^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$ \\ $$$$\left(\frac{\mathrm{7}}{\mathrm{2}}−{a}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}−{b}\right)^{\mathrm{2}} =\left({r}+\frac{\mathrm{5}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$$\left(−\frac{\mathrm{3}}{\mathrm{2}}−{a}\right)^{\mathrm{2}} +\left(\mathrm{3}−{b}\right)^{\mathrm{2}} =\left({r}+\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$$\left(−\mathrm{3}−{a}\right)^{\mathrm{2}} +\left(\mathrm{0}−{b}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$$\left({i}\right)−\left({iii}\right): \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}{a}\right)\left(\frac{\mathrm{13}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}{b}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{5}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{2}{r}+\frac{\mathrm{5}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\mathrm{26}{a}+\mathrm{2}{b}=−\mathrm{10}\sqrt{\mathrm{2}}{r}−\mathrm{18}\:\:\:…\left({I}\right) \\ $$$$\left({ii}\right)−\left({iii}\right): \\ $$$$\left(−\frac{\mathrm{9}}{\mathrm{2}}−\mathrm{2}{a}\right)\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\left(\mathrm{3}−\mathrm{2}{b}\right)\left(\mathrm{3}\right)=\frac{\mathrm{5}}{\mathrm{2}}\left(\mathrm{2}{r}+\frac{\mathrm{5}}{\mathrm{2}}\right) \\ $$$$\mathrm{3}{a}+\mathrm{6}{b}=−\mathrm{5}{r}−\mathrm{4}\:\:\:…\left({II}\right) \\ $$$$\Rightarrow{a}=−\frac{\left(\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{1}\right){r}}{\mathrm{15}}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{b}=\frac{\left(\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{13}\right){r}}{\mathrm{15}}−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${put}\:{into}\:\left({iii}\right): \\ $$$$\left(\frac{\left(\mathrm{6}\sqrt{\mathrm{2}}−\mathrm{1}\right){r}}{\mathrm{15}}−\frac{\mathrm{7}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{\left(\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{13}\right){r}}{\mathrm{15}}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\mathrm{18}\sqrt{\mathrm{2}}−\mathrm{7}\right){r}^{\mathrm{2}} +\left(\mathrm{90}\sqrt{\mathrm{2}}−\mathrm{40}\right){r}−\mathrm{250}=\mathrm{0} \\ $$$${r}=\frac{−\mathrm{45}\sqrt{\mathrm{2}}+\mathrm{20}\pm\mathrm{30}\sqrt{\mathrm{3}+\mathrm{3}\sqrt{\mathrm{2}}}}{\mathrm{18}\sqrt{\mathrm{2}}−\mathrm{7}} \\ $$$$\left({negative}\:{value}\:{for}\:{the}\:{big}\:{one}\right) \\ $$

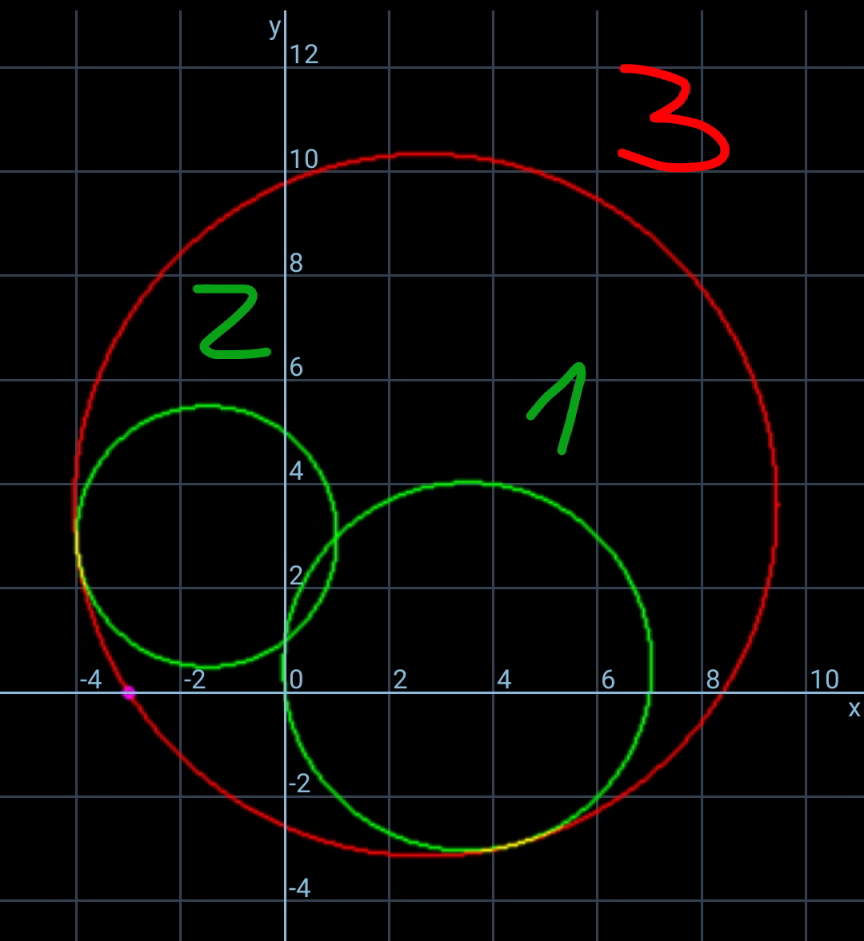
Commented by mr W last updated on 27/May/21