Question Number 10656 by okhema last updated on 22/Feb/17

$${find}\:{the}\:{equation}\:{of}\:{the}\:{circle}\:{with}\:{diameter}\:{AB}\:{where}\:{A}\:{is}\:{at}\:\left(\mathrm{2},\mathrm{4}\right)\:{and}\:{B}\:{is}\:{at}\:\left(−\mathrm{1},\mathrm{6}\right) \\ $$
Answered by FilupS last updated on 22/Feb/17
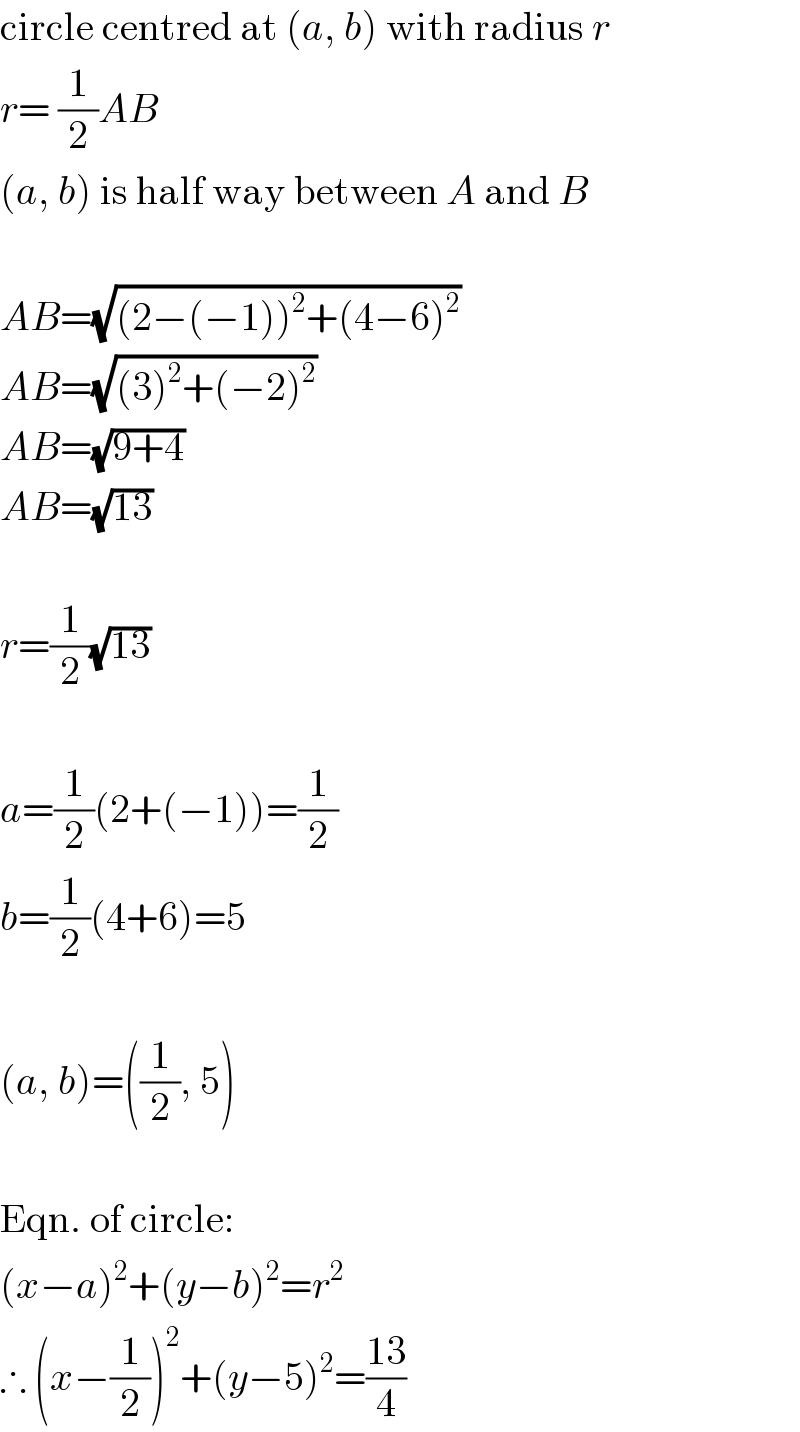
$$\mathrm{circle}\:\mathrm{centred}\:\mathrm{at}\:\left({a},\:{b}\right)\:\mathrm{with}\:\mathrm{radius}\:{r} \\ $$$${r}=\:\frac{\mathrm{1}}{\mathrm{2}}{AB} \\ $$$$\left({a},\:{b}\right)\:\mathrm{is}\:\mathrm{half}\:\mathrm{way}\:\mathrm{between}\:{A}\:\mathrm{and}\:{B} \\ $$$$\: \\ $$$${AB}=\sqrt{\left(\mathrm{2}−\left(−\mathrm{1}\right)\right)^{\mathrm{2}} +\left(\mathrm{4}−\mathrm{6}\right)^{\mathrm{2}} } \\ $$$${AB}=\sqrt{\left(\mathrm{3}\right)^{\mathrm{2}} +\left(−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$${AB}=\sqrt{\mathrm{9}+\mathrm{4}} \\ $$$${AB}=\sqrt{\mathrm{13}} \\ $$$$\: \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{13}} \\ $$$$\: \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}+\left(−\mathrm{1}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${b}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}+\mathrm{6}\right)=\mathrm{5} \\ $$$$\: \\ $$$$\left({a},\:{b}\right)=\left(\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{5}\right) \\ $$$$\: \\ $$$$\mathrm{Eqn}.\:\mathrm{of}\:\mathrm{circle}: \\ $$$$\left({x}−{a}\right)^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\therefore\:\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−\mathrm{5}\right)^{\mathrm{2}} =\frac{\mathrm{13}}{\mathrm{4}} \\ $$
Commented by okhema last updated on 22/Feb/17

$${thank}\:{you} \\ $$
