Question Number 10391 by 314159 last updated on 06/Feb/17
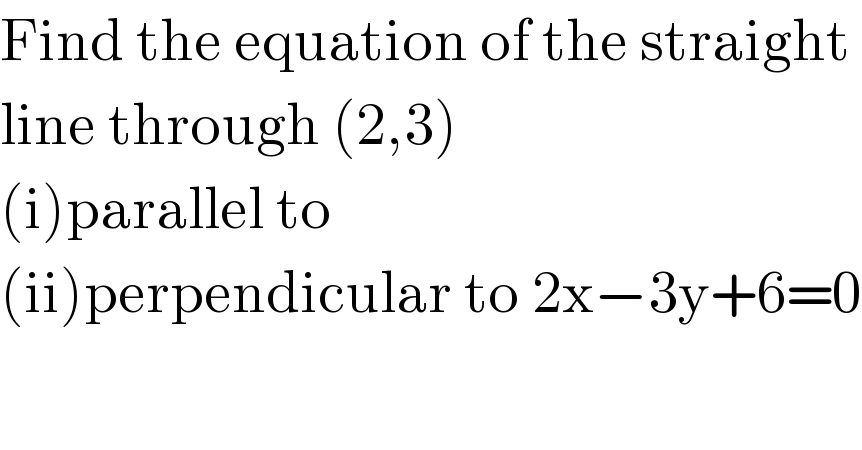
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{straight} \\ $$$$\mathrm{line}\:\mathrm{through}\:\left(\mathrm{2},\mathrm{3}\right)\: \\ $$$$\left(\mathrm{i}\right)\mathrm{parallel}\:\mathrm{to} \\ $$$$\left(\mathrm{ii}\right)\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{2x}−\mathrm{3y}+\mathrm{6}=\mathrm{0} \\ $$
Answered by mrW1 last updated on 06/Feb/17
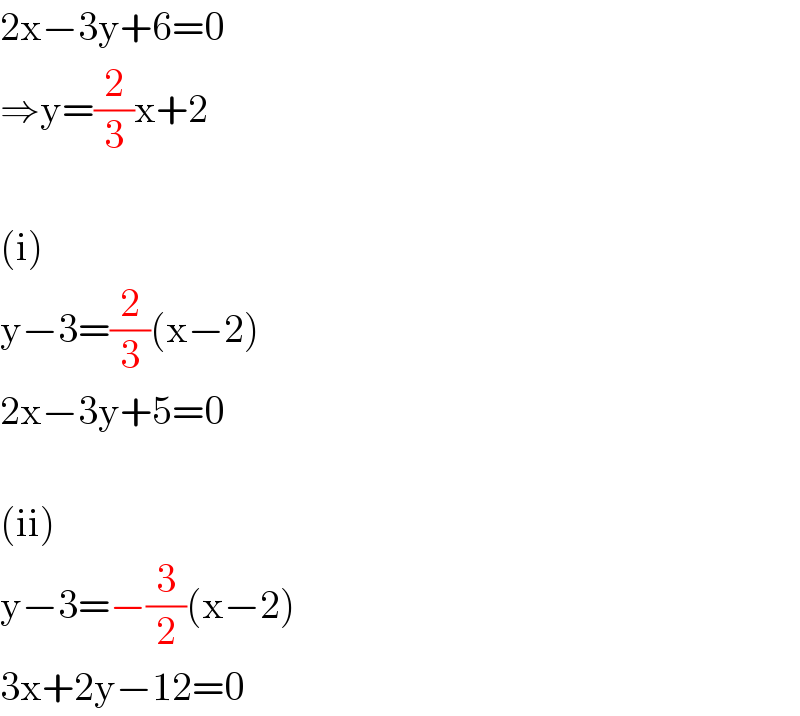
$$\mathrm{2x}−\mathrm{3y}+\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{x}+\mathrm{2} \\ $$$$ \\ $$$$\left(\mathrm{i}\right) \\ $$$$\mathrm{y}−\mathrm{3}=\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{x}−\mathrm{2}\right) \\ $$$$\mathrm{2x}−\mathrm{3y}+\mathrm{5}=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{ii}\right) \\ $$$$\mathrm{y}−\mathrm{3}=−\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{x}−\mathrm{2}\right) \\ $$$$\mathrm{3x}+\mathrm{2y}−\mathrm{12}=\mathrm{0} \\ $$
