Question Number 133587 by bemath last updated on 23/Feb/21
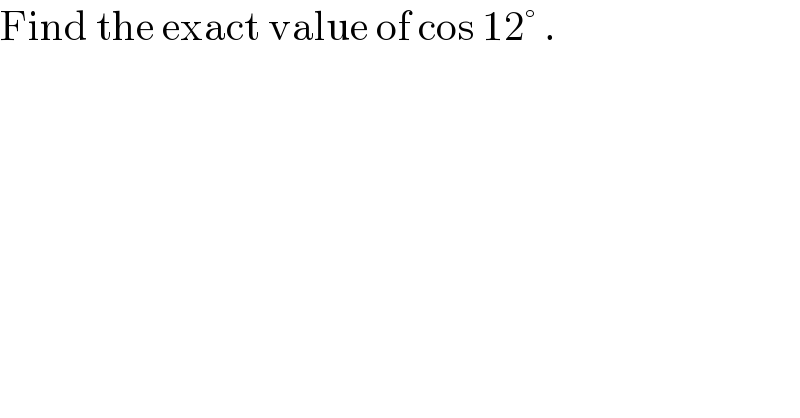
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{value}\:\mathrm{of}\:\mathrm{cos}\:\mathrm{12}°\:. \\ $$
Answered by Dwaipayan Shikari last updated on 23/Feb/21
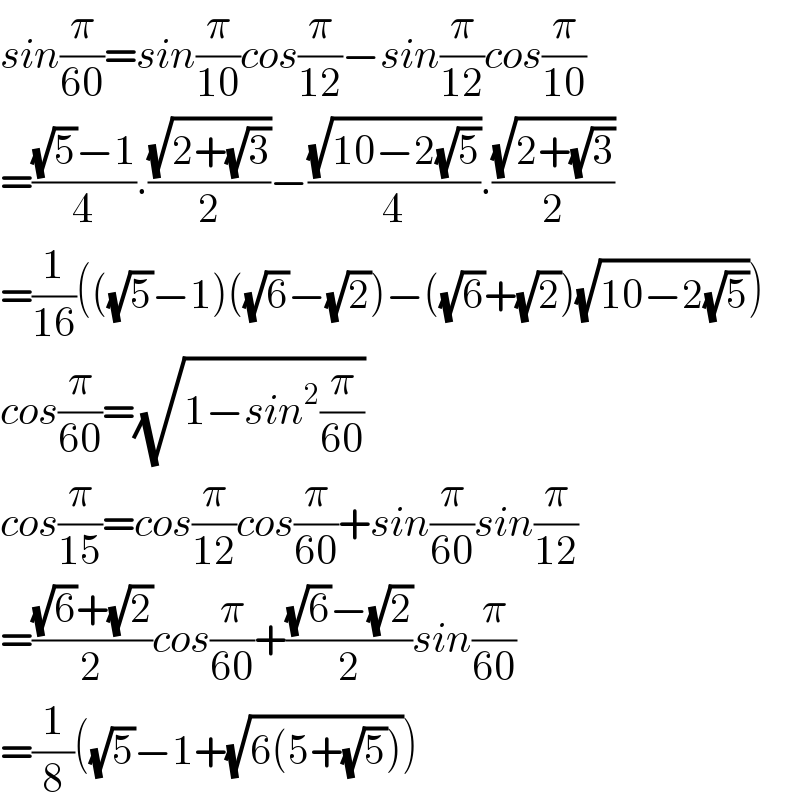
$${sin}\frac{\pi}{\mathrm{60}}={sin}\frac{\pi}{\mathrm{10}}{cos}\frac{\pi}{\mathrm{12}}−{sin}\frac{\pi}{\mathrm{12}}{cos}\frac{\pi}{\mathrm{10}} \\ $$$$=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}.\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}.\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left(\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\right)−\left(\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}\right) \\ $$$${cos}\frac{\pi}{\mathrm{60}}=\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{60}}} \\ $$$${cos}\frac{\pi}{\mathrm{15}}={cos}\frac{\pi}{\mathrm{12}}{cos}\frac{\pi}{\mathrm{60}}+{sin}\frac{\pi}{\mathrm{60}}{sin}\frac{\pi}{\mathrm{12}} \\ $$$$=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{2}}{cos}\frac{\pi}{\mathrm{60}}+\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{2}}{sin}\frac{\pi}{\mathrm{60}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\sqrt{\mathrm{5}}−\mathrm{1}+\sqrt{\mathrm{6}\left(\mathrm{5}+\sqrt{\mathrm{5}}\right)}\right) \\ $$
