Question Number 8789 by tawakalitu last updated on 27/Oct/16
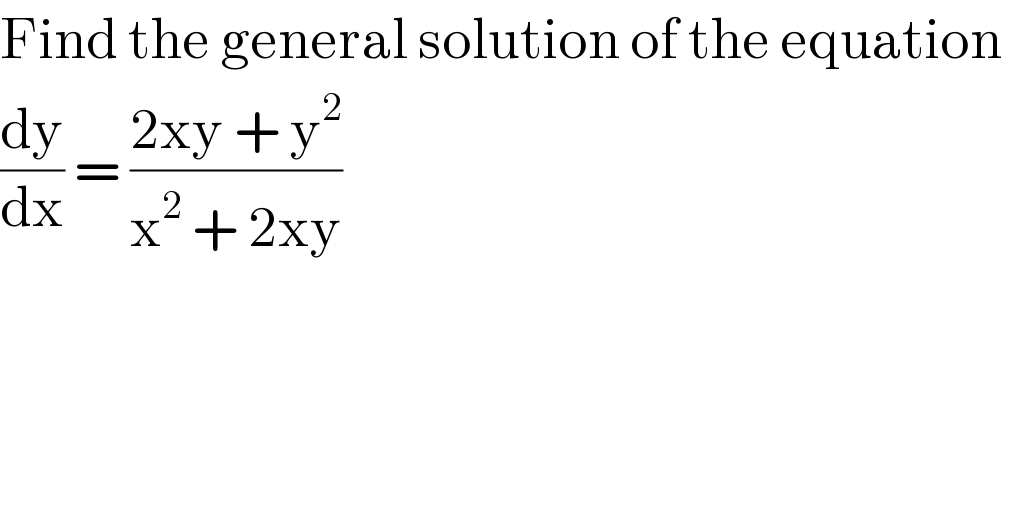
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{2xy}\:+\:\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{2xy}} \\ $$
Commented by Yozzias last updated on 27/Oct/16
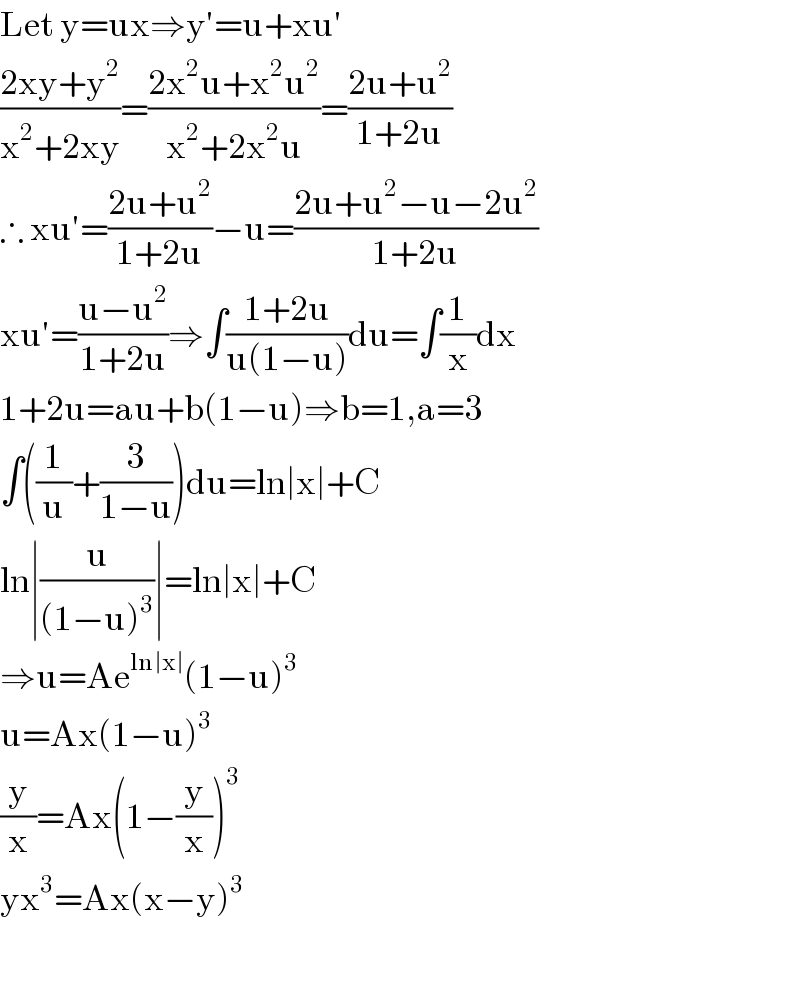
$$\mathrm{Let}\:\mathrm{y}=\mathrm{ux}\Rightarrow\mathrm{y}'=\mathrm{u}+\mathrm{xu}' \\ $$$$\frac{\mathrm{2xy}+\mathrm{y}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}}=\frac{\mathrm{2x}^{\mathrm{2}} \mathrm{u}+\mathrm{x}^{\mathrm{2}} \mathrm{u}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}^{\mathrm{2}} \mathrm{u}}=\frac{\mathrm{2u}+\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2u}} \\ $$$$\therefore\:\mathrm{xu}'=\frac{\mathrm{2u}+\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2u}}−\mathrm{u}=\frac{\mathrm{2u}+\mathrm{u}^{\mathrm{2}} −\mathrm{u}−\mathrm{2u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2u}} \\ $$$$\mathrm{xu}'=\frac{\mathrm{u}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{2u}}\Rightarrow\int\frac{\mathrm{1}+\mathrm{2u}}{\mathrm{u}\left(\mathrm{1}−\mathrm{u}\right)}\mathrm{du}=\int\frac{\mathrm{1}}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{1}+\mathrm{2u}=\mathrm{au}+\mathrm{b}\left(\mathrm{1}−\mathrm{u}\right)\Rightarrow\mathrm{b}=\mathrm{1},\mathrm{a}=\mathrm{3} \\ $$$$\int\left(\frac{\mathrm{1}}{\mathrm{u}}+\frac{\mathrm{3}}{\mathrm{1}−\mathrm{u}}\right)\mathrm{du}=\mathrm{ln}\mid\mathrm{x}\mid+\mathrm{C} \\ $$$$\mathrm{ln}\mid\frac{\mathrm{u}}{\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{3}} }\mid=\mathrm{ln}\mid\mathrm{x}\mid+\mathrm{C} \\ $$$$\Rightarrow\mathrm{u}=\mathrm{Ae}^{\mathrm{ln}\mid\mathrm{x}\mid} \left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{3}} \\ $$$$\mathrm{u}=\mathrm{Ax}\left(\mathrm{1}−\mathrm{u}\right)^{\mathrm{3}} \\ $$$$\frac{\mathrm{y}}{\mathrm{x}}=\mathrm{Ax}\left(\mathrm{1}−\frac{\mathrm{y}}{\mathrm{x}}\right)^{\mathrm{3}} \\ $$$$\mathrm{yx}^{\mathrm{3}} =\mathrm{Ax}\left(\mathrm{x}−\mathrm{y}\right)^{\mathrm{3}} \\ $$$$ \\ $$
Commented by tawakalitu last updated on 27/Oct/16
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
