Question Number 1134 by 314159 last updated on 28/Jun/15
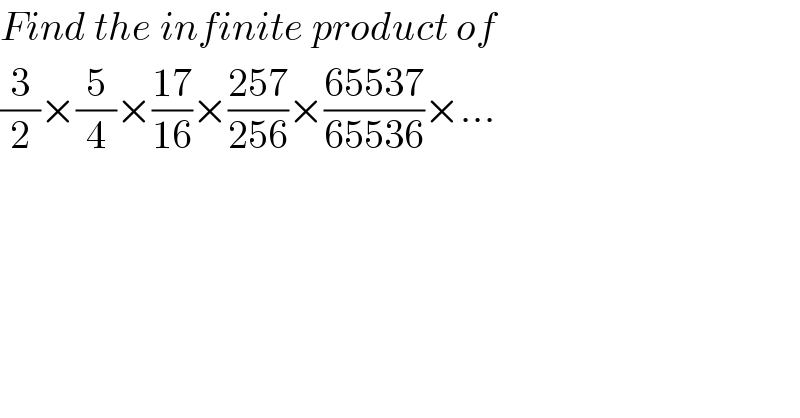
$${Find}\:{the}\:{infinite}\:{product}\:{of}\: \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{5}}{\mathrm{4}}×\frac{\mathrm{17}}{\mathrm{16}}×\frac{\mathrm{257}}{\mathrm{256}}×\frac{\mathrm{65537}}{\mathrm{65536}}×… \\ $$
Answered by prakash jain last updated on 29/Jun/15

$$\frac{\mathrm{2}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }=\frac{\mathrm{2}^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}^{\mathrm{3}} } \\ $$$$\frac{\mathrm{2}^{\mathrm{4}} −\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }×\frac{\mathrm{2}^{\mathrm{4}} +\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }=\frac{\mathrm{2}^{\mathrm{8}} −\mathrm{1}}{\mathrm{2}^{\mathrm{7}} } \\ $$$$\frac{\mathrm{2}^{\mathrm{8}} −\mathrm{1}}{\mathrm{2}^{\mathrm{7}} }×\frac{\mathrm{2}^{\mathrm{8}} +\mathrm{1}}{\mathrm{2}^{\mathrm{8}} }=\frac{\mathrm{2}^{\mathrm{16}} −\mathrm{1}}{\mathrm{2}^{\mathrm{15}} } \\ $$$${product}\:{to}\:{k}\:{terms}\:=\frac{\mathrm{2}^{\mathrm{2}^{\mathrm{2}{k}} } −\mathrm{1}}{\mathrm{2}^{\mathrm{2}^{\mathrm{2}{k}} −\mathrm{1}} }=\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}^{\mathrm{2}{k}} −\mathrm{1}} }\right) \\ $$$${k}\rightarrow\infty\:\mathrm{product}=\mathrm{2} \\ $$
Commented by 314159 last updated on 01/Jul/15

$$\boldsymbol{\mathrm{Thanks}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{lot}}\:\boldsymbol{\mathrm{Mr}}.\boldsymbol{\mathrm{Prakash}} \\ $$
