Question Number 2103 by Yozzi last updated on 02/Nov/15
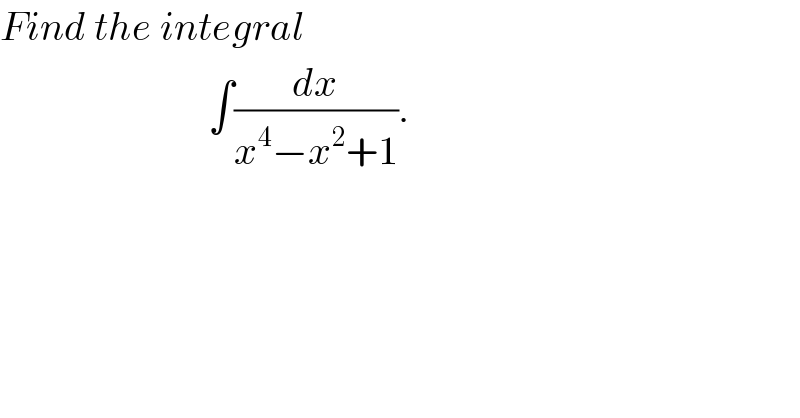
$${Find}\:{the}\:{integral} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int\frac{{dx}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}. \\ $$
Commented by Yozzi last updated on 02/Nov/15

$${Yup}. \\ $$
Commented by prakash jain last updated on 02/Nov/15
![one option. (1/(x^4 −x^2 +1))=(1/(x^4 −x^2 +(1/4)+(3/4))) =(1/((x^2 −(1/2))^2 −(((i(√3))/2))^2 )) =((1/(i(√3))))[(1/(x^2 −(1/2)−((i(√3))/2)))−(1/(x^2 −(1/2)+((i(√3))/2)))]](https://www.tinkutara.com/question/Q2106.png)
$$\mathrm{one}\:\mathrm{option}.\: \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\left(\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}}\right)\left[\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}−\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}}\right] \\ $$
Commented by Yozzi last updated on 03/Nov/15
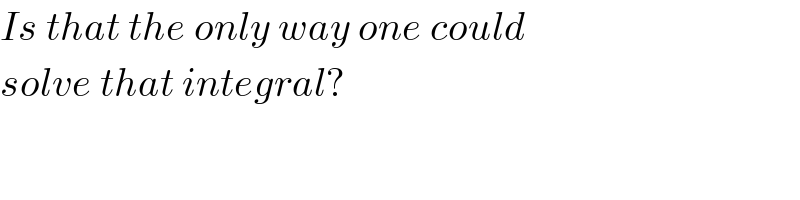
$${Is}\:{that}\:{the}\:{only}\:{way}\:{one}\:{could} \\ $$$${solve}\:{that}\:{integral}? \\ $$
Commented by prakash jain last updated on 03/Nov/15

$${x}=\mathrm{tan}\:{u} \\ $$$${dx}=\frac{{du}}{\mathrm{cos}^{\mathrm{2}} {u}} \\ $$$$\frac{\mathrm{1}}{\frac{\mathrm{sin}^{\mathrm{4}} {u}}{\mathrm{cos}^{\mathrm{2}} {u}}−\mathrm{sin}^{\mathrm{2}} {u}+\mathrm{1}}=\frac{\mathrm{cos}^{\mathrm{2}} {u}}{\mathrm{sin}^{\mathrm{4}} {u}−\mathrm{sin}^{\mathrm{2}} {u}\mathrm{cos}^{\mathrm{2}} {u}+\mathrm{cos}^{\mathrm{2}} {u}} \\ $$$$=\frac{\mathrm{2cos}^{\mathrm{2}} {u}}{\mathrm{2}−\left(\mathrm{sin}\:\mathrm{2}{u}\right)^{\mathrm{2}} } \\ $$$$\mathrm{This}\:\mathrm{can}\:\mathrm{be}\:\mathrm{integrated}\:\mathrm{without}\:\mathrm{using}\:{i}. \\ $$
Answered by prakash jain last updated on 03/Nov/15
![(d/du)sin 2u=2(cos2u)=2(2cos^2 u−1) dy=2cos2udu= ((2cos^2 u)/(2−(sin 2u)^2 ))=(1/2)[((2(2cos^2 u−1))/(2−(sin 2u)^2 ))+(2/(2−(sin 2u)^2 ))] part Awill inegrate to ln ((√2)−sin 2u)−ln ((√2)+sin 2u) (2/(2−(sin2u)^2 )) to be done](https://www.tinkutara.com/question/Q2125.png)
$$\frac{{d}}{{du}}\mathrm{sin}\:\mathrm{2}{u}=\mathrm{2}\left(\mathrm{cos2}{u}\right)=\mathrm{2}\left(\mathrm{2cos}^{\mathrm{2}} {u}−\mathrm{1}\right) \\ $$$${dy}=\mathrm{2cos2}{udu}= \\ $$$$\frac{\mathrm{2cos}^{\mathrm{2}} {u}}{\mathrm{2}−\left(\mathrm{sin}\:\mathrm{2}{u}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{2}\left(\mathrm{2cos}^{\mathrm{2}} {u}−\mathrm{1}\right)}{\mathrm{2}−\left(\mathrm{sin}\:\mathrm{2}{u}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{2}−\left(\mathrm{sin}\:\mathrm{2}{u}\right)^{\mathrm{2}} }\right] \\ $$$${part}\:{Awill}\:{inegrate}\:{to} \\ $$$$\mathrm{ln}\:\left(\sqrt{\mathrm{2}}−\mathrm{sin}\:\mathrm{2}{u}\right)−\mathrm{ln}\:\left(\sqrt{\mathrm{2}}+\mathrm{sin}\:\mathrm{2}{u}\right) \\ $$$$ \\ $$$$\frac{\mathrm{2}}{\mathrm{2}−\left(\mathrm{sin2}{u}\right)^{\mathrm{2}} \:}\:{to}\:{be}\:{done} \\ $$
Commented by prakash jain last updated on 03/Nov/15
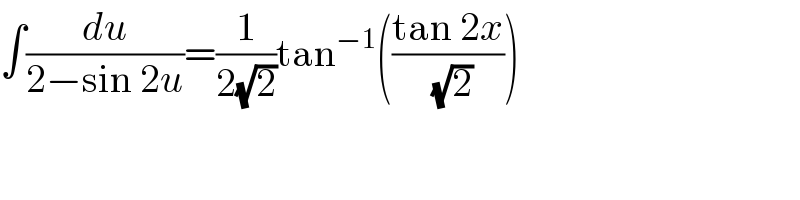
$$\int\frac{{du}}{\mathrm{2}−\mathrm{sin}\:\mathrm{2}{u}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\mathrm{2}{x}}{\:\sqrt{\mathrm{2}}}\right) \\ $$
