Question Number 2069 by Yozzi last updated on 01/Nov/15

$${Find}\:{the}\:{integral} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int\left({xcosh}\left({lnx}\right)\right)^{{n}} {dx} \\ $$$${where}\:{n}=\mathrm{0},\mathrm{1},\mathrm{2},… \\ $$
Commented by prakash jain last updated on 01/Nov/15
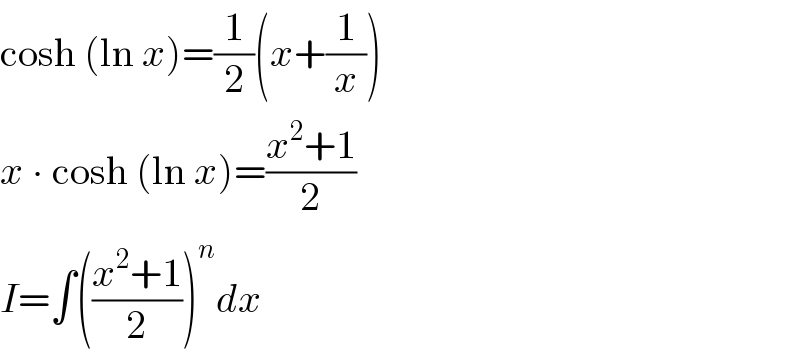
$$\mathrm{cosh}\:\left(\mathrm{ln}\:{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\frac{\mathrm{1}}{{x}}\right) \\ $$$${x}\:\centerdot\:\mathrm{cosh}\:\left(\mathrm{ln}\:{x}\right)=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}} \\ $$$${I}=\int\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}\right)^{{n}} {dx} \\ $$
Answered by prakash jain last updated on 01/Nov/15
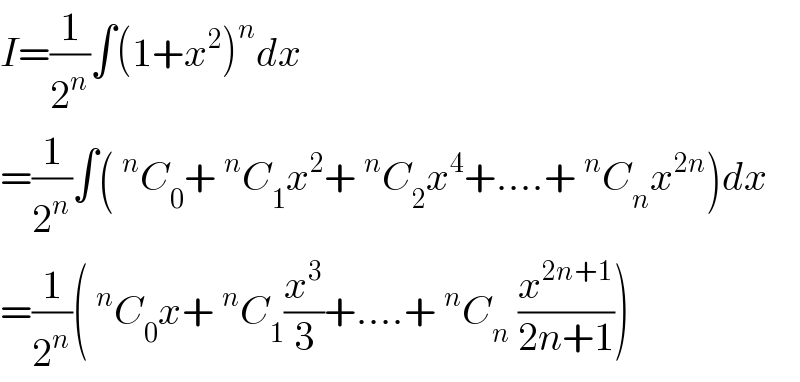
$${I}=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\int\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\int\left(\:^{{n}} {C}_{\mathrm{0}} +\:^{{n}} {C}_{\mathrm{1}} {x}^{\mathrm{2}} +\:^{{n}} {C}_{\mathrm{2}} {x}^{\mathrm{4}} +….+\:^{{n}} {C}_{{n}} {x}^{\mathrm{2}{n}} \right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\left(\:^{{n}} {C}_{\mathrm{0}} {x}+\:^{{n}} {C}_{\mathrm{1}} \frac{{x}^{\mathrm{3}} }{\mathrm{3}}+….+\:^{{n}} {C}_{{n}} \:\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$
