Find-the-maximum-area-of-an-isosceles-triangle-inscribed-in-an-ellipse-x-2-a-2-y-2-b-2-1with-its-vetrex-at-one-end-of-the-major-axis-

Question Number 76077 by vishalbhardwaj last updated on 23/Dec/19

Find the maximum area of an isosceles triangle

inscribed in an ellipse \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 with its vetrex

at one end of the major axis ? ?

Commented by MJS last updated on 23/Dec/19

the centroid of the triangle is in the center

of the ellipse

the idea is :

construct a circle with r = a

insert an equilateral triangle with one vertex

in (\begin{matrix} a \\ 0 \end{matrix})

now multiply all y - values by \frac{b}{a}

\Rightarrow the circle becomes the ellipse

\Rightarrow the triangle becomes the one {you}^{'} re

searching

Commented by MJS last updated on 23/Dec/19

btw all triangles you construct this way,

out of an equilateral triangle, no matter

where you put the vertices on the circle

will share the same maximum area

Commented by vishalbhardwaj last updated on 23/Dec/19

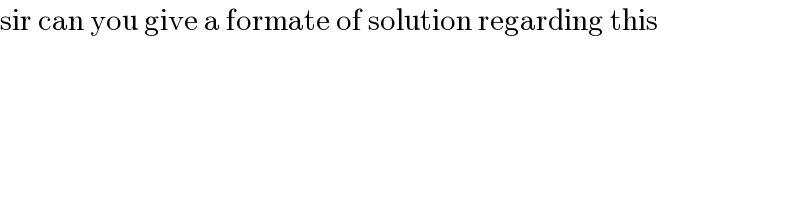
sir can you give a formate of solution regarding this

Answered by MJS last updated on 23/Dec/19

equilateral triangle in circle with radius a

A = (\begin{matrix} a \\ 0 \end{matrix}) B = (\begin{matrix} - \frac{a}{2} \\ \frac{a \sqrt{3}}{2} \end{matrix}) C = (\begin{matrix} - \frac{a}{2} \\ - \frac{a \sqrt{3}}{2} \end{matrix})

x^{*} = x; y^{*} = \frac{b}{a} y

A^{*} = (\begin{matrix} a \\ 0 \end{matrix}) B^{*} = (\begin{matrix} - \frac{a}{2} \\ \frac{b \sqrt{3}}{2} \end{matrix}) C^{*} = (\begin{matrix} - \frac{a}{2} \\ - \frac{b \sqrt{3}}{2} \end{matrix})

area A B C = \frac{3 a^{2} \sqrt{3}}{4}

area A^{*} B^{*} C^{*} = \frac{3 a b \sqrt{3}}{4}

side lengths B^{*} C^{*} = b \sqrt{3}; A^{*} B^{*} = C^{*} A^{*} = \frac{\sqrt{3}}{2} \sqrt{3 a^{2} + b^{2}}

Commented by vishalbhardwaj last updated on 23/Dec/19

Dear sir, can we solve this question by using

differentiation (maxima and minima condition)

Answered by MJS last updated on 23/Dec/19

A = (\begin{matrix} a \\ 0 \end{matrix}) B = (\begin{matrix} x \\ \frac{b}{a} \sqrt{a^{2} - x^{2}} \end{matrix}) C = (\begin{matrix} x \\ - \frac{b}{a} \sqrt{a^{2} - x^{2}} \end{matrix})

∣ A B ∣^{2} =∣ C A ∣^{2} = (x - a) (x - \frac{a (a^{2} + b^{2})}{a^{2} - b^{2}})

∣ B C ∣^{2} = \frac{4 b^{2}}{a^{2}} (a^{2} - x^{2})

area (o, p, q) =

= \frac{1}{4} \sqrt{(o + p + q) (- o + p + q) (o - p + q) (o + p - q)}

= \frac{1}{4} \sqrt{2 (o^{2} p^{2} + o^{2} q^{2} + p^{2} q^{2} - (o^{4} + p^{4} + q^{4})}

area (o, p, p) = \frac{1}{4} o \sqrt{4 p^{2} - o^{2}}

o^{2} = \frac{4 b^{2}}{a^{2}} (a^{2} - x^{2}) \land p^{2} = (x - a) (x - \frac{a (a^{2} + b^{2})}{a^{2} - b^{2}})

area (o, p, p) = \frac{b}{a} ∣ x - a ∣ \sqrt{a^{2} - x^{2}}

\frac{d}{d x} [\frac{b}{a} ∣ x - a ∣ \sqrt{a^{2} - x^{2}}] = \pm \frac{b (2 x^{2} - a x - a^{2})}{a \sqrt{a^{2} - x^{3}}} = 0

\Rightarrow x = - \frac{a}{2}

Facebook Tweet Pin