Question Number 137597 by bemath last updated on 04/Apr/21

$$ \\ $$Find the minimum value of x^(2) +y^(2) +z^(2) , subject to the condition 2x+3y+5z=30?
Answered by EDWIN88 last updated on 04/Apr/21

Answered by mr W last updated on 04/Apr/21
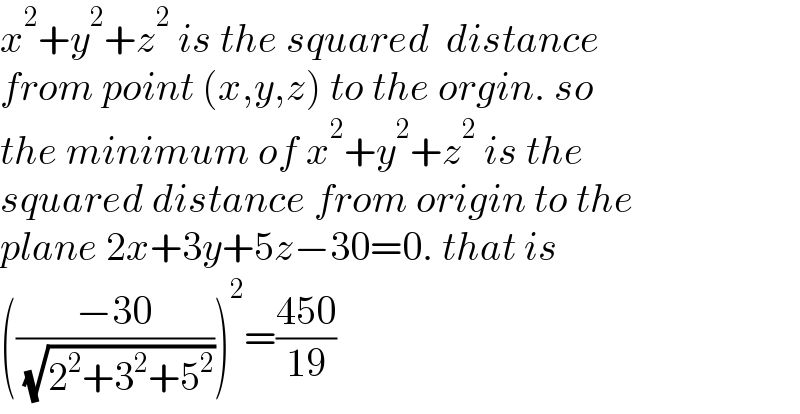
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:{is}\:{the}\:{squared}\:\:{distance} \\ $$$${from}\:{point}\:\left({x},{y},{z}\right)\:{to}\:{the}\:{orgin}.\:{so} \\ $$$${the}\:{minimum}\:{of}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:{is}\:{the} \\ $$$${squared}\:{distance}\:{from}\:{origin}\:{to}\:{the} \\ $$$${plane}\:\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{5}{z}−\mathrm{30}=\mathrm{0}.\:{that}\:{is} \\ $$$$\left(\frac{−\mathrm{30}}{\:\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }}\right)^{\mathrm{2}} =\frac{\mathrm{450}}{\mathrm{19}} \\ $$
Commented by otchereabdullai@gmail.com last updated on 04/Apr/21

$$\mathrm{nice}\:\mathrm{shortcut} \\ $$
