Question Number 8996 by Basant007 last updated on 11/Nov/16
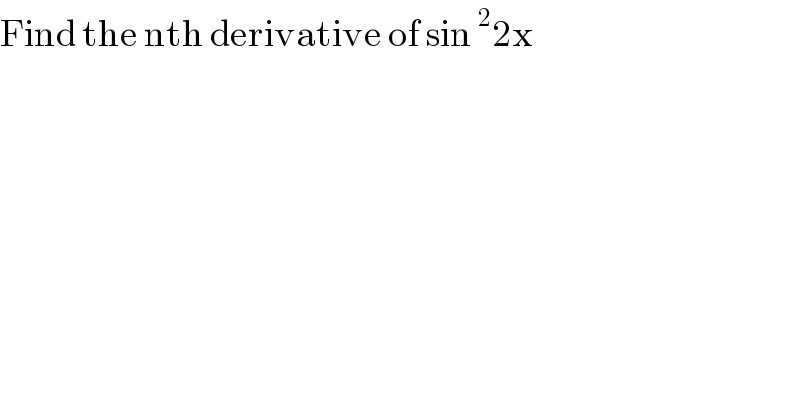
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{nth}\:\mathrm{derivative}\:\mathrm{of}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{2x} \\ $$
Commented by FilupSmith last updated on 13/Nov/16
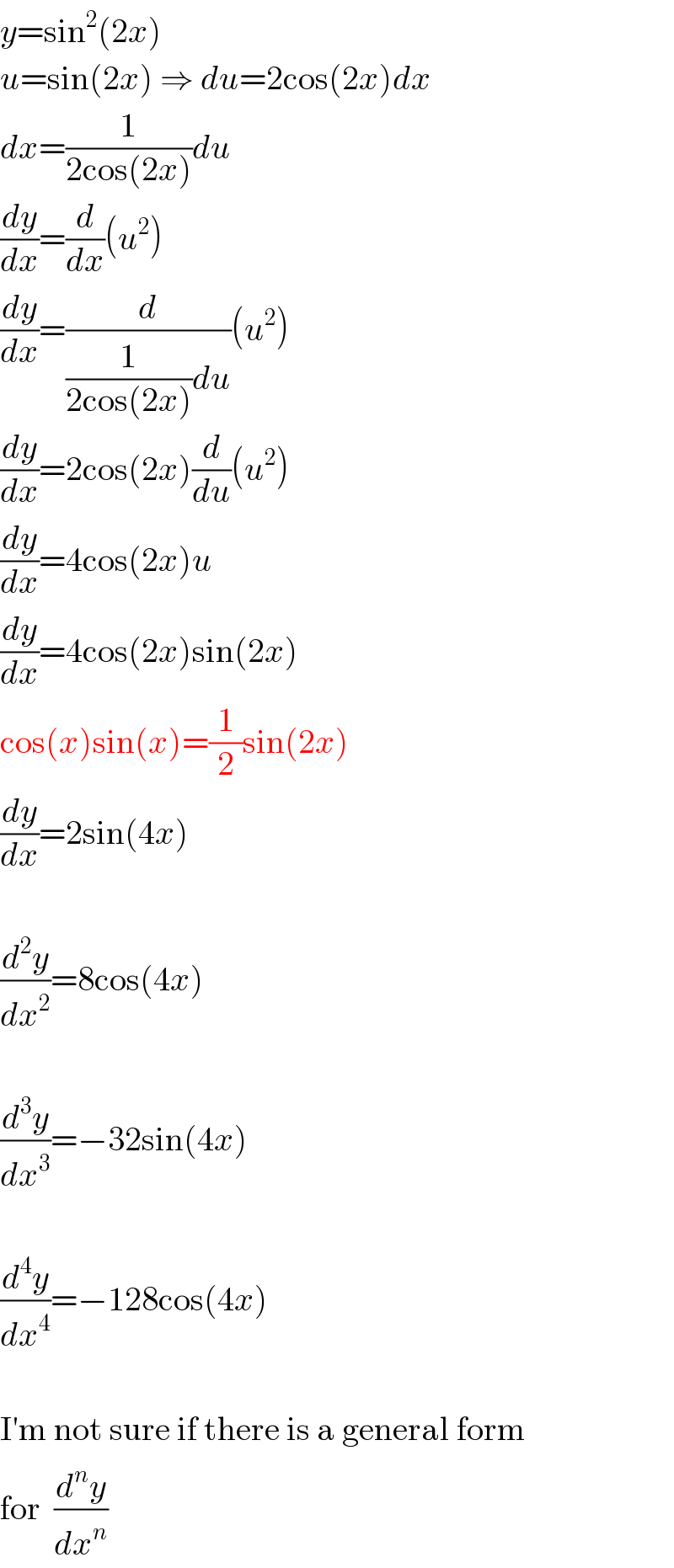
$${y}=\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right) \\ $$$${u}=\mathrm{sin}\left(\mathrm{2}{x}\right)\:\Rightarrow\:{du}=\mathrm{2cos}\left(\mathrm{2}{x}\right){dx} \\ $$$${dx}=\frac{\mathrm{1}}{\mathrm{2cos}\left(\mathrm{2}{x}\right)}{du} \\ $$$$\frac{{dy}}{{dx}}=\frac{{d}}{{dx}}\left({u}^{\mathrm{2}} \right) \\ $$$$\frac{{dy}}{{dx}}=\frac{{d}}{\frac{\mathrm{1}}{\mathrm{2cos}\left(\mathrm{2}{x}\right)}{du}}\left({u}^{\mathrm{2}} \right) \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2cos}\left(\mathrm{2}{x}\right)\frac{{d}}{{du}}\left({u}^{\mathrm{2}} \right) \\ $$$$\frac{{dy}}{{dx}}=\mathrm{4cos}\left(\mathrm{2}{x}\right){u} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{4cos}\left(\mathrm{2}{x}\right)\mathrm{sin}\left(\mathrm{2}{x}\right) \\ $$$$\mathrm{cos}\left({x}\right)\mathrm{sin}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}{x}\right) \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2sin}\left(\mathrm{4}{x}\right) \\ $$$$\: \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{8cos}\left(\mathrm{4}{x}\right) \\ $$$$\: \\ $$$$\frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} }=−\mathrm{32sin}\left(\mathrm{4}{x}\right) \\ $$$$\: \\ $$$$\frac{{d}^{\mathrm{4}} {y}}{{dx}^{\mathrm{4}} }=−\mathrm{128cos}\left(\mathrm{4}{x}\right) \\ $$$$\: \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{there}\:\mathrm{is}\:\mathrm{a}\:\mathrm{general}\:\mathrm{form} \\ $$$$\mathrm{for}\:\:\frac{{d}^{{n}} {y}}{{dx}^{{n}} } \\ $$
Answered by 123456 last updated on 14/Nov/16
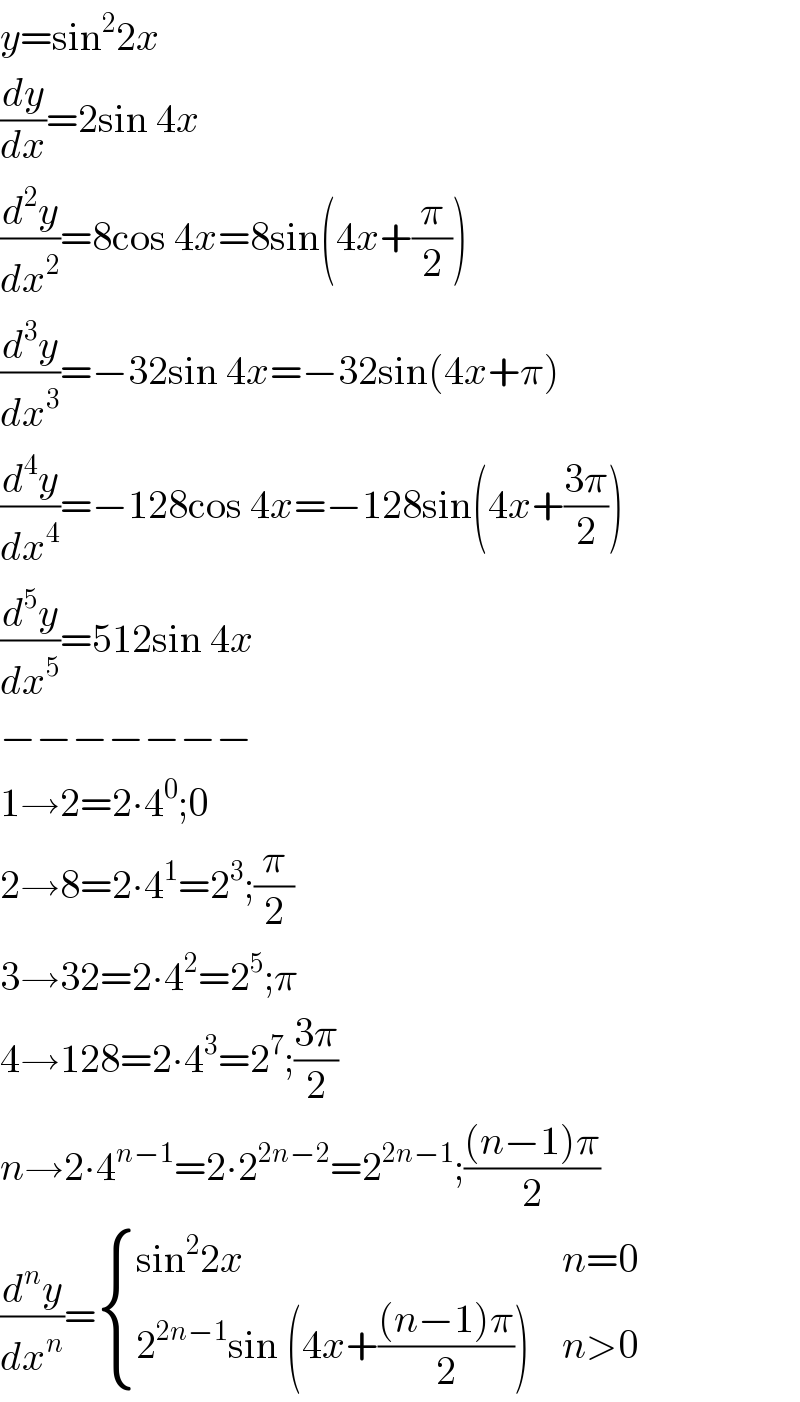
$${y}=\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{2sin}\:\mathrm{4}{x} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{8cos}\:\mathrm{4}{x}=\mathrm{8sin}\left(\mathrm{4}{x}+\frac{\pi}{\mathrm{2}}\right) \\ $$$$\frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} }=−\mathrm{32sin}\:\mathrm{4}{x}=−\mathrm{32sin}\left(\mathrm{4}{x}+\pi\right) \\ $$$$\frac{{d}^{\mathrm{4}} {y}}{{dx}^{\mathrm{4}} }=−\mathrm{128cos}\:\mathrm{4}{x}=−\mathrm{128sin}\left(\mathrm{4}{x}+\frac{\mathrm{3}\pi}{\mathrm{2}}\right) \\ $$$$\frac{{d}^{\mathrm{5}} {y}}{{dx}^{\mathrm{5}} }=\mathrm{512sin}\:\mathrm{4}{x} \\ $$$$−−−−−−− \\ $$$$\mathrm{1}\rightarrow\mathrm{2}=\mathrm{2}\centerdot\mathrm{4}^{\mathrm{0}} ;\mathrm{0} \\ $$$$\mathrm{2}\rightarrow\mathrm{8}=\mathrm{2}\centerdot\mathrm{4}^{\mathrm{1}} =\mathrm{2}^{\mathrm{3}} ;\frac{\pi}{\mathrm{2}}\: \\ $$$$\mathrm{3}\rightarrow\mathrm{32}=\mathrm{2}\centerdot\mathrm{4}^{\mathrm{2}} =\mathrm{2}^{\mathrm{5}} ;\pi \\ $$$$\mathrm{4}\rightarrow\mathrm{128}=\mathrm{2}\centerdot\mathrm{4}^{\mathrm{3}} =\mathrm{2}^{\mathrm{7}} ;\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$${n}\rightarrow\mathrm{2}\centerdot\mathrm{4}^{{n}−\mathrm{1}} =\mathrm{2}\centerdot\mathrm{2}^{\mathrm{2}{n}−\mathrm{2}} =\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} ;\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}} \\ $$$$\frac{{d}^{{n}} {y}}{{dx}^{{n}} }=\begin{cases}{\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}}&{{n}=\mathrm{0}}\\{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} \mathrm{sin}\:\left(\mathrm{4}{x}+\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}}\right)}&{{n}>\mathrm{0}}\end{cases} \\ $$
