Find-the-number-of-terms-in-1-x-101-1-x-2-x-100-

Question Number 855 by 112358 last updated on 26/Mar/15

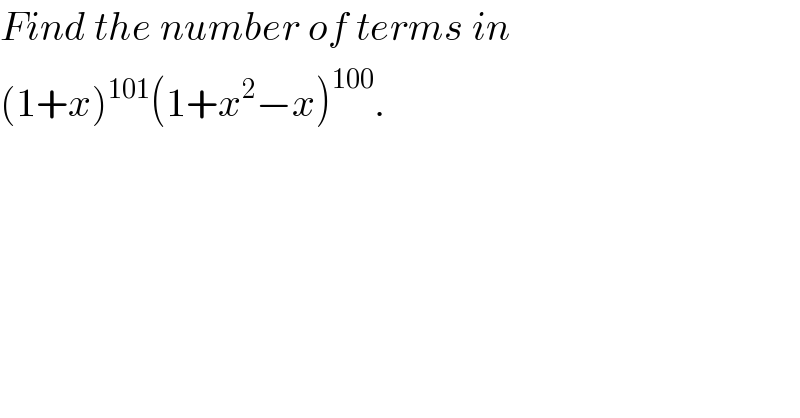
F i n d t h e n u m b e r o f t e r m s i n

{(1 + x)}^{101} {(1 + x^{2} - x)}^{100} .

Answered by prakash jain last updated on 26/Mar/15

= {[(1 + x) (1 + x^{2} - x)]}^{100} (1 + x)

= {[1 + x^{2} - x + x + x^{3} - x^{2}]}^{100} (1 + x)

= {[1 + x^{3}]}^{100} (1 + x) = {(1 + x^{3})}^{100} + x {(1 + x^{3})}^{300}

{(1 + x^{3})}^{100} = \underset{i = 0}{\sum^{100}}^{100} C_{i} x^{3 i} (101 t e r m s) \dots (i)

x {(1 + x^{3})}^{100} = \underset{i = 0}{\sum^{100}}^{100} C_{i} x^{3 i + 1} (101 t e r m s) \dots (i i)

Total number of terms = 202 since no

common terms in (i) and (i i) .