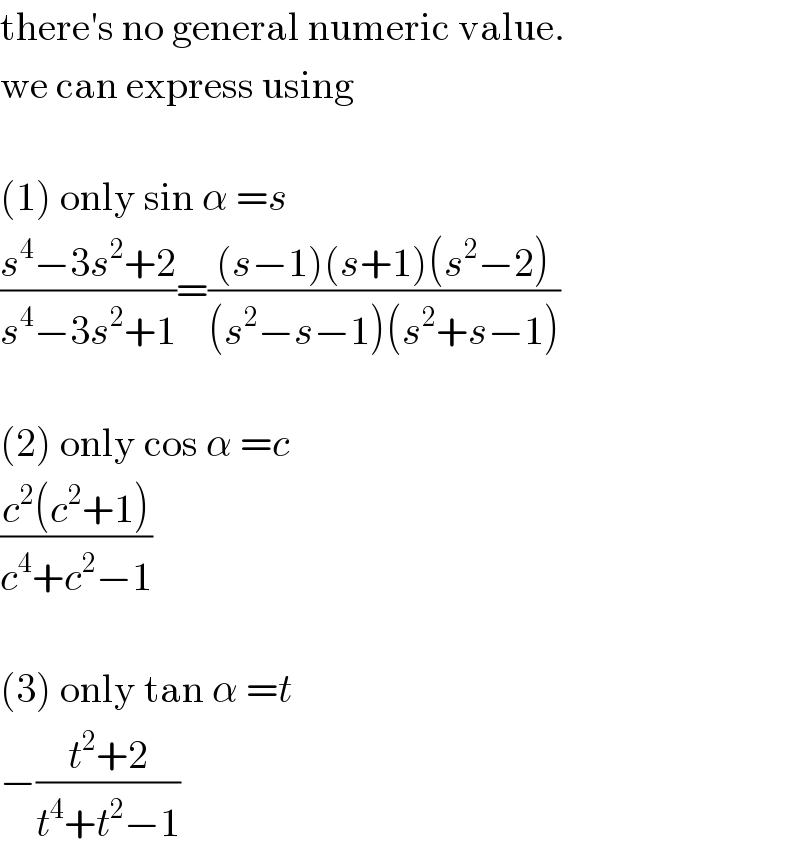Find-the-numeric-value-of-2-sin-2-cos-2-tan-2-

Question Number 72931 by Maclaurin Stickker last updated on 05/Nov/19

F i n d t h e n u m e r i c v a l u e o f

\frac{2 - \sin^{2} (α)}{\cos^{2} (α) - \tan^{2} (α)}

Answered by ajfour last updated on 05/Nov/19

s a y α = 0 °

n u m e r i c v a l u e = \frac{2}{1} = 2

s a y α = 45 °

n u m e r i c v a l u e = \frac{2 - \frac{1}{2}}{\frac{1}{2} - 1} = - 3 .

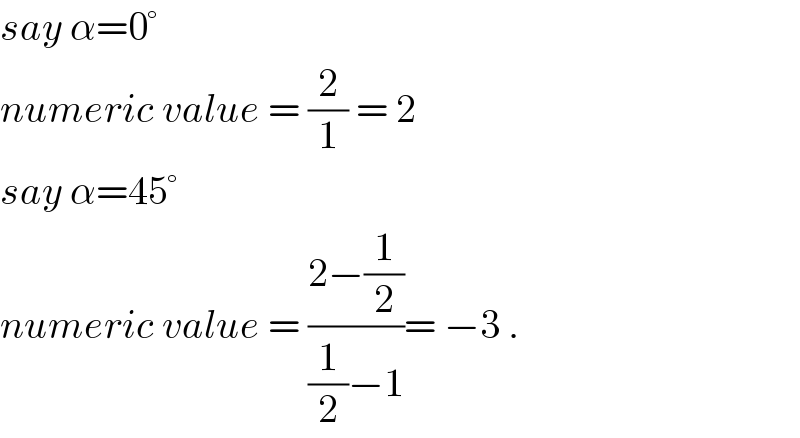
Commented by Maclaurin Stickker last updated on 05/Nov/19

C a n y o u s o l v e b y f a c t o r i n g

t h e e x p r e s s i o n ?

Commented by ajfour last updated on 05/Nov/19

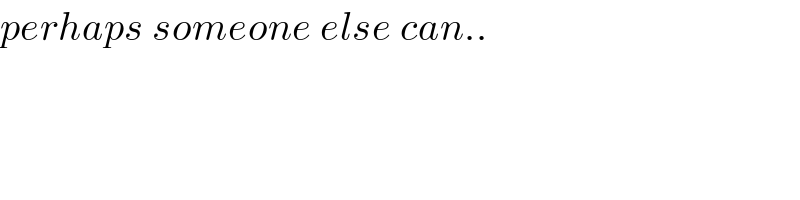
p e r h a p s s o m e o n e e l s e c a n . .

Answered by MJS last updated on 05/Nov/19

{there}^{'} s no general numeric value .

we can express using

(1) only \sin α = s

\frac{s^{4} - 3 s^{2} + 2}{s^{4} - 3 s^{2} + 1} = \frac{(s - 1) (s + 1) (s^{2} - 2)}{(s^{2} - s - 1) (s^{2} + s - 1)}

(2) only \cos α = c

\frac{c^{2} (c^{2} + 1)}{c^{4} + c^{2} - 1}

(3) only \tan α = t

- \frac{t^{2} + 2}{t^{4} + t^{2} - 1}

Facebook Tweet Pin