Question Number 143131 by mohammad17 last updated on 10/Jun/21
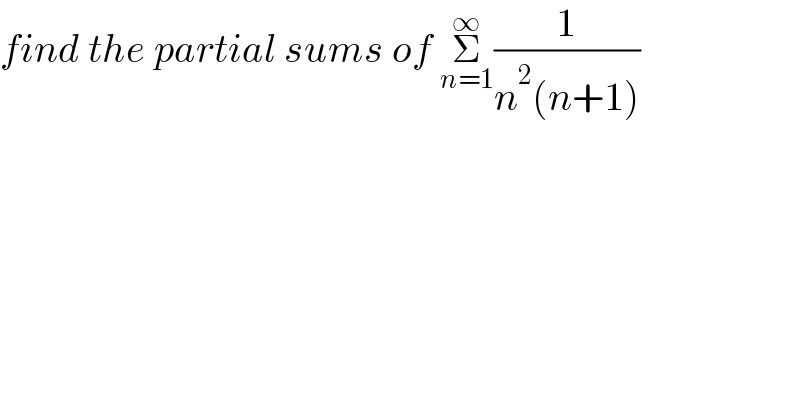
$${find}\:{the}\:{partial}\:{sums}\:{of}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)} \\ $$
Answered by qaz last updated on 10/Jun/21
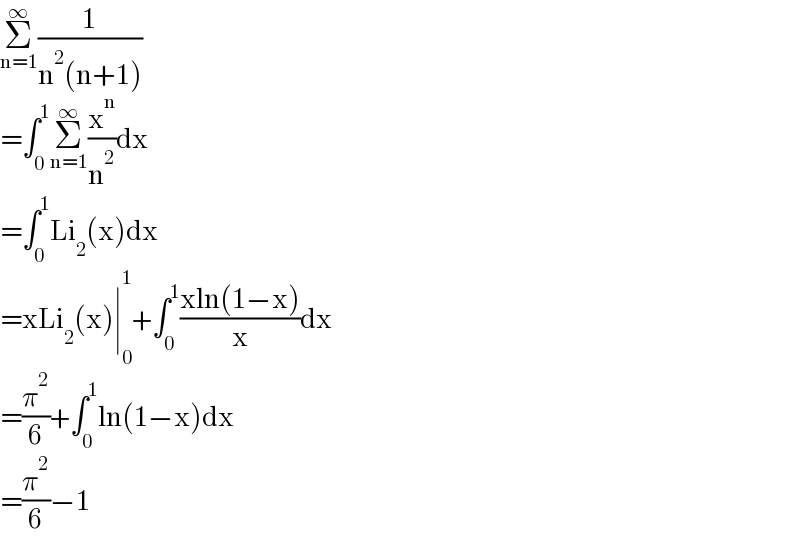
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx} \\ $$$$=\mathrm{xLi}_{\mathrm{2}} \left(\mathrm{x}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{xln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1} \\ $$
Commented by mohammad17 last updated on 11/Jun/21
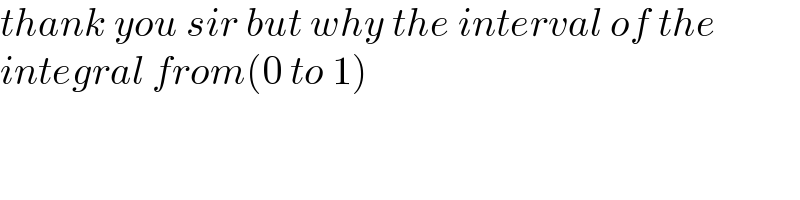
$${thank}\:{you}\:{sir}\:{but}\:{why}\:{the}\:{interval}\:{of}\:{the} \\ $$$${integral}\:{from}\left(\mathrm{0}\:{to}\:\mathrm{1}\right) \\ $$
Answered by Olaf_Thorendsen last updated on 10/Jun/21
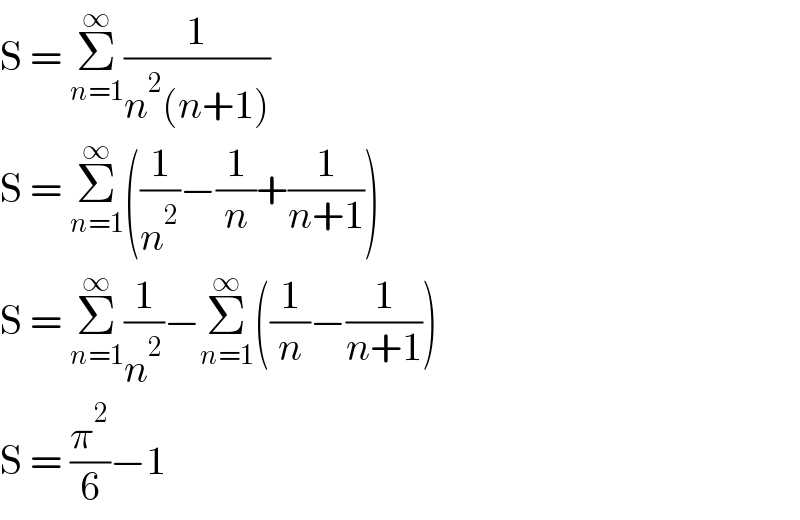
$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$\mathrm{S}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1} \\ $$
