Question Number 5592 by Rasheed Soomro last updated on 21/May/16
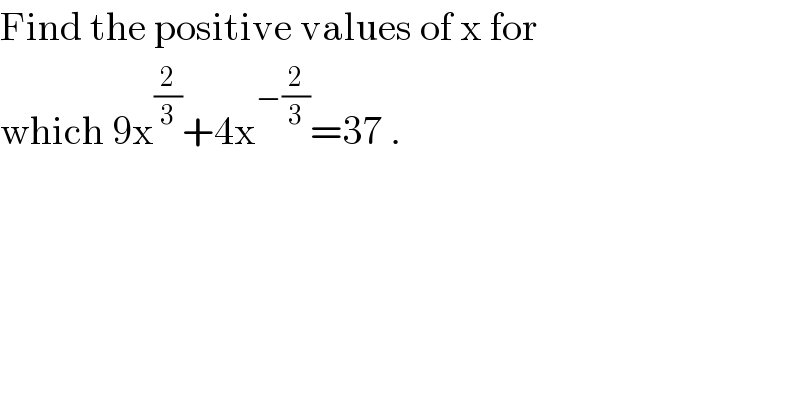
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{positive}\:\mathrm{values}\:\mathrm{of}\:\mathrm{x}\:\mathrm{for} \\ $$$$\mathrm{which}\:\mathrm{9x}^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{4x}^{−\frac{\mathrm{2}}{\mathrm{3}}} =\mathrm{37}\:. \\ $$
Answered by prakash jain last updated on 21/May/16

$${y}={x}^{\mathrm{2}/\mathrm{3}} \\ $$$$\mathrm{9}{y}+\frac{\mathrm{4}}{{y}}=\mathrm{37} \\ $$$$\mathrm{9}{y}^{\mathrm{2}} −\mathrm{37}{y}+\mathrm{4}=\mathrm{0} \\ $$$$\left(\mathrm{9}{y}−\mathrm{1}\right)\left({y}−\mathrm{4}\right)=\mathrm{0} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{9}}\:{or}\:{y}=\mathrm{4} \\ $$$${x}^{\mathrm{2}/\mathrm{3}} =\mathrm{1}/\mathrm{9} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{6}} }\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{27}} \\ $$$$\mathrm{similary}\:\mathrm{second}\:\mathrm{solution}\:{x}=\mathrm{8} \\ $$
