Question Number 72499 by Mr Jor last updated on 29/Oct/19
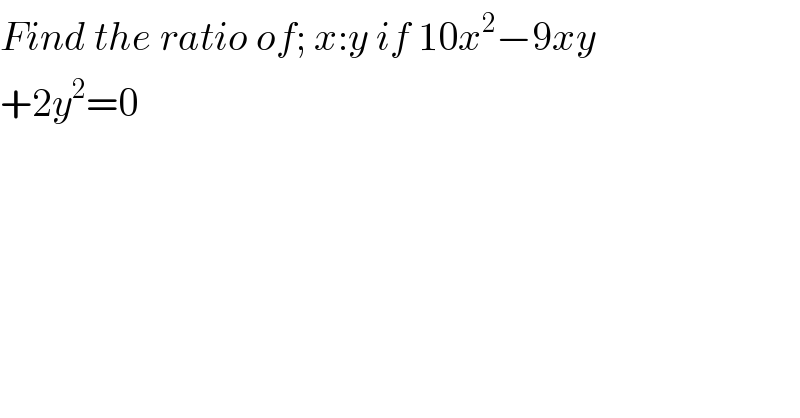
$${Find}\:{the}\:{ratio}\:{of};\:{x}:{y}\:{if}\:\mathrm{10}{x}^{\mathrm{2}} −\mathrm{9}{xy} \\ $$$$+\mathrm{2}{y}^{\mathrm{2}} =\mathrm{0} \\ $$
Answered by Tanmay chaudhury last updated on 29/Oct/19
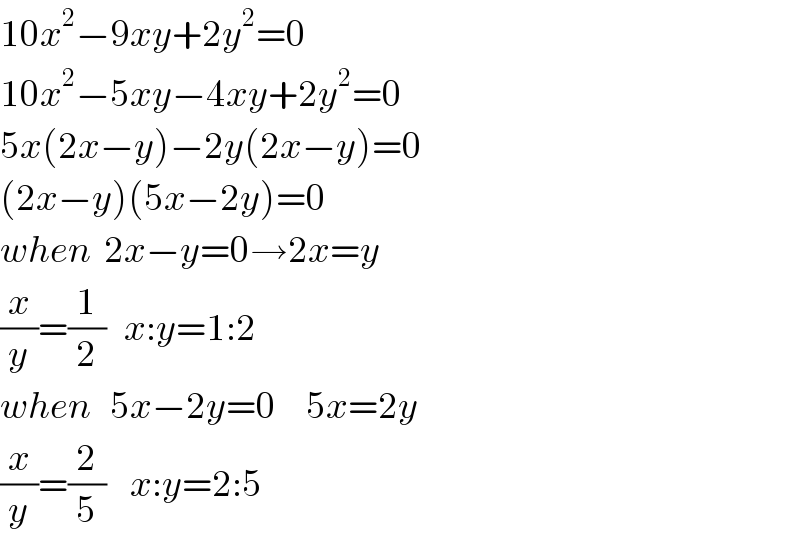
$$\mathrm{10}{x}^{\mathrm{2}} −\mathrm{9}{xy}+\mathrm{2}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{10}{x}^{\mathrm{2}} −\mathrm{5}{xy}−\mathrm{4}{xy}+\mathrm{2}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{5}{x}\left(\mathrm{2}{x}−{y}\right)−\mathrm{2}{y}\left(\mathrm{2}{x}−{y}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}{x}−{y}\right)\left(\mathrm{5}{x}−\mathrm{2}{y}\right)=\mathrm{0} \\ $$$${when}\:\:\mathrm{2}{x}−{y}=\mathrm{0}\rightarrow\mathrm{2}{x}={y} \\ $$$$\frac{{x}}{{y}}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:{x}:{y}=\mathrm{1}:\mathrm{2} \\ $$$${when}\:\:\:\mathrm{5}{x}−\mathrm{2}{y}=\mathrm{0}\:\:\:\:\:\mathrm{5}{x}=\mathrm{2}{y} \\ $$$$\frac{{x}}{{y}}=\frac{\mathrm{2}}{\mathrm{5}}\:\:\:\:{x}:{y}=\mathrm{2}:\mathrm{5} \\ $$
Answered by $@ty@m123 last updated on 29/Oct/19
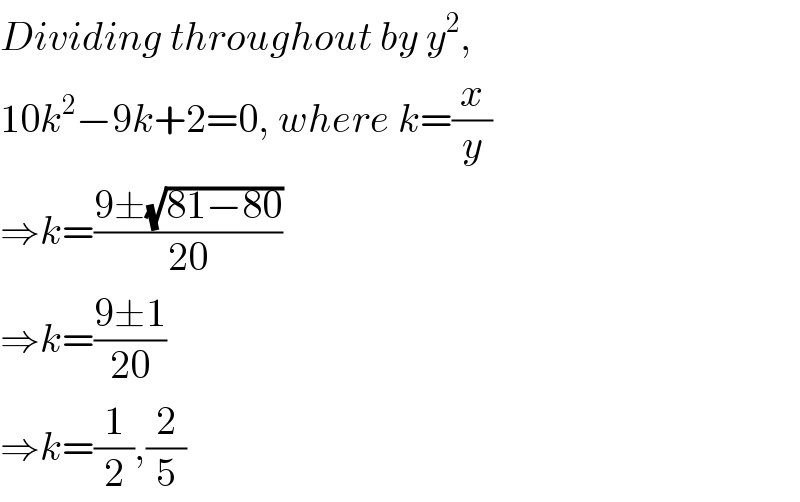
$${Dividing}\:{throughout}\:{by}\:{y}^{\mathrm{2}} , \\ $$$$\mathrm{10}{k}^{\mathrm{2}} −\mathrm{9}{k}+\mathrm{2}=\mathrm{0},\:{where}\:{k}=\frac{{x}}{{y}} \\ $$$$\Rightarrow{k}=\frac{\mathrm{9}\pm\sqrt{\mathrm{81}−\mathrm{80}}}{\mathrm{20}} \\ $$$$\Rightarrow{k}=\frac{\mathrm{9}\pm\mathrm{1}}{\mathrm{20}} \\ $$$$\Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{2}}{\mathrm{5}} \\ $$
Answered by MJS last updated on 29/Oct/19
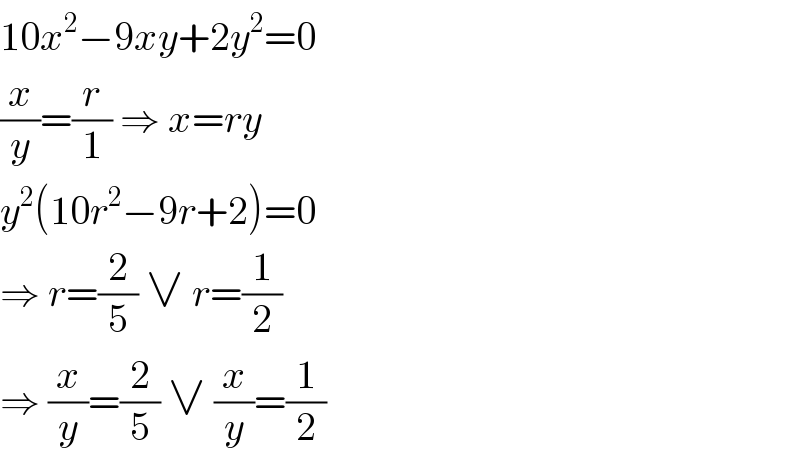
$$\mathrm{10}{x}^{\mathrm{2}} −\mathrm{9}{xy}+\mathrm{2}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{{x}}{{y}}=\frac{{r}}{\mathrm{1}}\:\Rightarrow\:{x}={ry} \\ $$$${y}^{\mathrm{2}} \left(\mathrm{10}{r}^{\mathrm{2}} −\mathrm{9}{r}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{r}=\frac{\mathrm{2}}{\mathrm{5}}\:\vee\:{r}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{{x}}{{y}}=\frac{\mathrm{2}}{\mathrm{5}}\:\vee\:\frac{{x}}{{y}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
