Question Number 137364 by liberty last updated on 02/Apr/21

$${Find}\:{the}\:{remainder}\:\mathrm{7}^{\mathrm{30}} \:{divide} \\ $$$${by}\:\mathrm{10}\: \\ $$
Answered by MJS_new last updated on 02/Apr/21
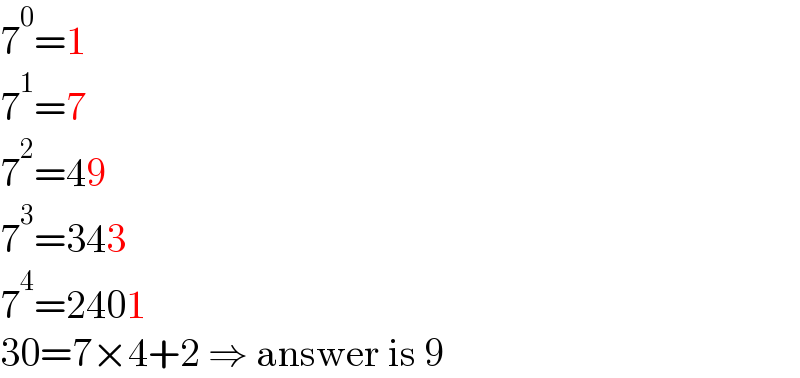
$$\mathrm{7}^{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{7}^{\mathrm{1}} =\mathrm{7} \\ $$$$\mathrm{7}^{\mathrm{2}} =\mathrm{49} \\ $$$$\mathrm{7}^{\mathrm{3}} =\mathrm{343} \\ $$$$\mathrm{7}^{\mathrm{4}} =\mathrm{2401} \\ $$$$\mathrm{30}=\mathrm{7}×\mathrm{4}+\mathrm{2}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{9} \\ $$
Answered by EDWIN88 last updated on 02/Apr/21

$$\mathrm{we}\:\mathrm{have}\:\mathrm{7}^{\mathrm{30}} \:=\:\mathrm{49}^{\mathrm{15}} \:\equiv\:\mathrm{9}^{\mathrm{15}} \:\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{apply}\:\mathrm{Binomial}\:\mathrm{Theorem} \\ $$$$ \:\mathrm{9}^{\mathrm{15}} \:=\:\left(\mathrm{10}−\mathrm{1}\right)^{\mathrm{15}} \:=\:\underset{\mathrm{k}\:=\:\mathrm{0}} {\overset{\mathrm{15}} {\sum}}\begin{pmatrix}{\mathrm{15}}\\{\:\:\mathrm{k}}\end{pmatrix}\:\mathrm{10}^{\mathrm{15}−\mathrm{k}} .\left(−\mathrm{1}\right)^{\mathrm{k}} \: \\ $$$$\mathrm{so}\:\mathrm{clearly}\:\mathrm{9}^{\mathrm{15}} \:\equiv\:−\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{10}\right)\:=\:\mathrm{9}\:\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\mathrm{therefore}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{7}^{\mathrm{30}} \::\:\mathrm{10}\:\mathrm{is}\:\mathrm{equal} \\ $$$$\mathrm{to}\:\mathrm{9}\:. \\ $$
Answered by benjo_mathlover last updated on 02/Apr/21

$${By}\:{Euler}\:{phi}\:{Theorem}\: \\ $$$$\mathrm{7}^{\varphi\left({n}\right)} \:=\:\mathrm{1}\:\left({mod}\:{n}\right)\: \\ $$$${we}\:{find}\:\varphi\left(\mathrm{10}\right)\:=\:\mathrm{10}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}\right)=\mathrm{4} \\ $$$${so}\:\mathrm{7}^{\mathrm{30}} \:=\:\left(\mathrm{7}^{\mathrm{4}} \right)^{\mathrm{7}} ×\mathrm{7}^{\mathrm{2}} \:=\:\mathrm{1}×\mathrm{7}^{\mathrm{2}} \:\left({mod}\:\mathrm{10}\right) \\ $$$$=\:\mathrm{49}\:\left({mod}\:\mathrm{10}\right)\:=\:\mathrm{9}\:\left({mod}\:\mathrm{10}\right) \\ $$$${it}\:{follows}\:{that}\:{the}\:{remainder} \\ $$$${is}\:\mathrm{9}\: \\ $$
