Question Number 7859 by tawakalitu last updated on 21/Sep/16
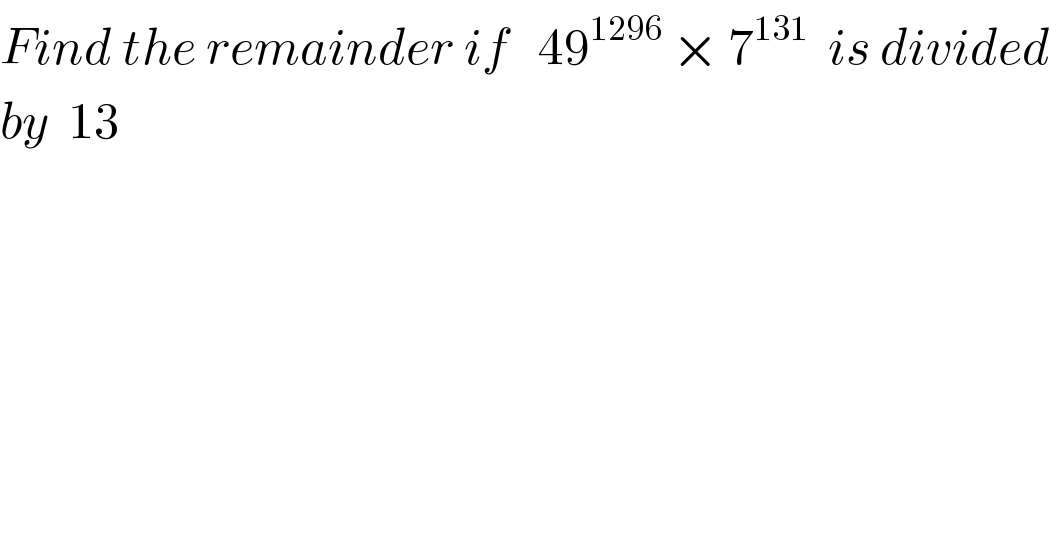
$${Find}\:{the}\:{remainder}\:{if}\:\:\:\mathrm{49}^{\mathrm{1296}} \:×\:\mathrm{7}^{\mathrm{131}} \:\:{is}\:{divided} \\ $$$${by}\:\:\mathrm{13}\:\: \\ $$
Answered by sandy_suhendra last updated on 21/Sep/16
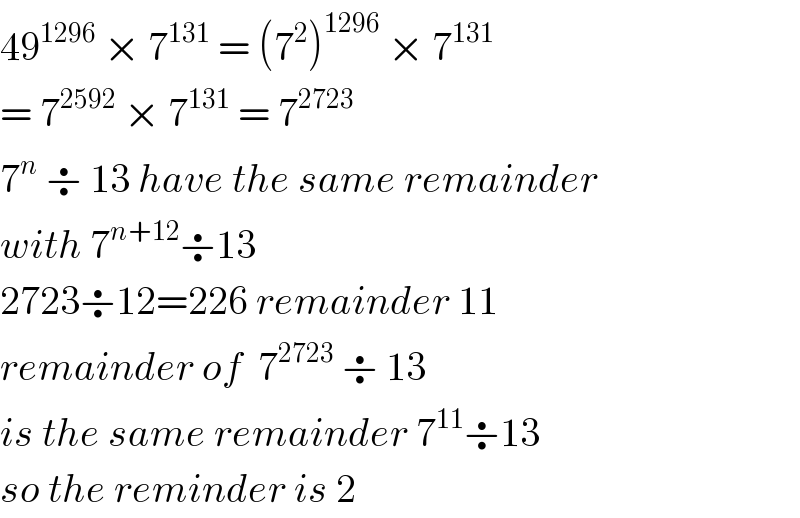
$$\mathrm{49}^{\mathrm{1296}} \:×\:\mathrm{7}^{\mathrm{131}} \:=\:\left(\mathrm{7}^{\mathrm{2}} \right)^{\mathrm{1296}} \:×\:\mathrm{7}^{\mathrm{131}} \\ $$$$=\:\mathrm{7}^{\mathrm{2592}} \:×\:\mathrm{7}^{\mathrm{131}} \:=\:\mathrm{7}^{\mathrm{2723}} \\ $$$$\mathrm{7}^{{n}} \:\boldsymbol{\div}\:\mathrm{13}\:{have}\:{the}\:{same}\:{remainder} \\ $$$${with}\:\mathrm{7}^{{n}+\mathrm{12}} \boldsymbol{\div}\mathrm{13} \\ $$$$\mathrm{2723}\boldsymbol{\div}\mathrm{12}=\mathrm{226}\:{remainder}\:\mathrm{11} \\ $$$${remainder}\:{of}\:\:\mathrm{7}^{\mathrm{2723}} \:\boldsymbol{\div}\:\mathrm{13}\: \\ $$$${is}\:{the}\:{same}\:{remainder}\:\mathrm{7}^{\mathrm{11}} \boldsymbol{\div}\mathrm{13} \\ $$$${so}\:{the}\:{reminder}\:{is}\:\mathrm{2} \\ $$
