Menu Close

Find-the-remainder-when-x-x-25-x-49-x-81-is-divided-by-x-3-1-

Tinku Tara 0 Comments
Pin




Question Number 77655 by TawaTawa last updated on 08/Jan/20
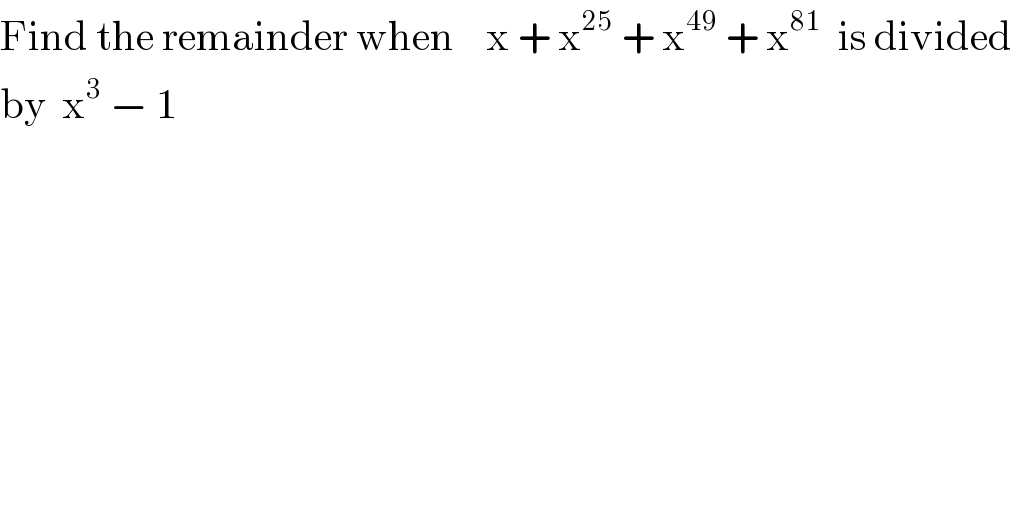
Find the remainder when x + x^(25) + x^(49) + x^(81) is divided by x^3 − 1
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{when}\:\:\:\:\mathrm{x}\:+\:\mathrm{x}^{\mathrm{25}} \:+\:\mathrm{x}^{\mathrm{49}} \:+\:\mathrm{x}^{\mathrm{81}} \:\:\mathrm{is}\:\mathrm{divided} \\ $$$$\mathrm{by}\:\:\mathrm{x}^{\mathrm{3}} \:−\:\mathrm{1} \\ $$
Commented by jagoll last updated on 08/Jan/20
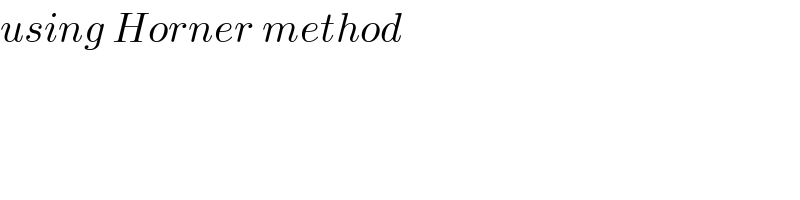
using Horner method
$${using}\:{Horner}\:{method} \\ $$
Answered by mind is power last updated on 09/Jan/20
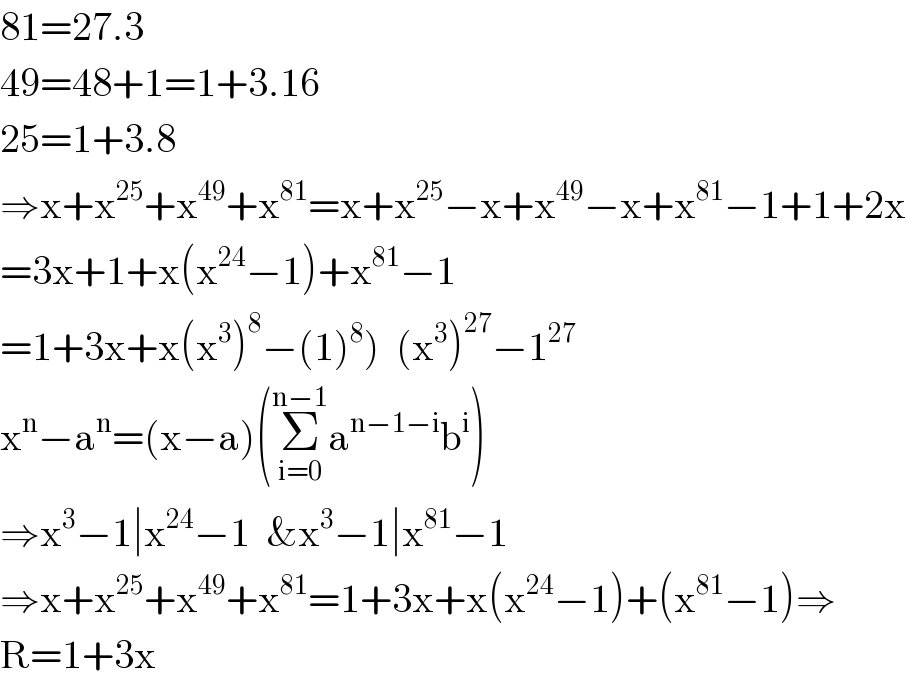
81=27.3 49=48+1=1+3.16 25=1+3.8 ⇒x+x^(25) +x^(49) +x^(81) =x+x^(25) −x+x^(49) −x+x^(81) −1+1+2x =3x+1+x(x^(24) −1)+x^(81) −1 =1+3x+x(x^3 )^8 −(1)^8 ) (x^3 )^(27) −1^(27) x^n −a^n =(x−a)(Σ_(i=0) ^(n−1) a^(n−1−i) b^i ) ⇒x^3 −1∣x^(24) −1 &x^3 −1∣x^(81) −1 ⇒x+x^(25) +x^(49) +x^(81) =1+3x+x(x^(24) −1)+(x^(81) −1)⇒ R=1+3x
$$\mathrm{81}=\mathrm{27}.\mathrm{3} \\ $$$$\mathrm{49}=\mathrm{48}+\mathrm{1}=\mathrm{1}+\mathrm{3}.\mathrm{16} \\ $$$$\mathrm{25}=\mathrm{1}+\mathrm{3}.\mathrm{8} \\ $$$$\Rightarrow\mathrm{x}+\mathrm{x}^{\mathrm{25}} +\mathrm{x}^{\mathrm{49}} +\mathrm{x}^{\mathrm{81}} =\mathrm{x}+\mathrm{x}^{\mathrm{25}} −\mathrm{x}+\mathrm{x}^{\mathrm{49}} −\mathrm{x}+\mathrm{x}^{\mathrm{81}} −\mathrm{1}+\mathrm{1}+\mathrm{2x} \\ $$$$=\mathrm{3x}+\mathrm{1}+\mathrm{x}\left(\mathrm{x}^{\mathrm{24}} −\mathrm{1}\right)+\mathrm{x}^{\mathrm{81}} −\mathrm{1} \\ $$$$\left.=\mathrm{1}+\mathrm{3x}+\mathrm{x}\left(\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{8}} −\left(\mathrm{1}\right)^{\mathrm{8}} \right)\:\:\left(\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{27}} −\mathrm{1}^{\mathrm{27}} \\ $$$$\mathrm{x}^{\mathrm{n}} −\mathrm{a}^{\mathrm{n}} =\left(\mathrm{x}−\mathrm{a}\right)\left(\underset{\mathrm{i}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{a}^{\mathrm{n}−\mathrm{1}−\mathrm{i}} \mathrm{b}^{\mathrm{i}} \right) \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{3}} −\mathrm{1}\mid\mathrm{x}^{\mathrm{24}} −\mathrm{1}\:\:\&\mathrm{x}^{\mathrm{3}} −\mathrm{1}\mid\mathrm{x}^{\mathrm{81}} −\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}+\mathrm{x}^{\mathrm{25}} +\mathrm{x}^{\mathrm{49}} +\mathrm{x}^{\mathrm{81}} =\mathrm{1}+\mathrm{3x}+\mathrm{x}\left(\mathrm{x}^{\mathrm{24}} −\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{81}} −\mathrm{1}\right)\Rightarrow \\ $$$$\mathrm{R}=\mathrm{1}+\mathrm{3x} \\ $$
Commented by TawaTawa last updated on 09/Jan/20
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by john santu last updated on 09/Jan/20
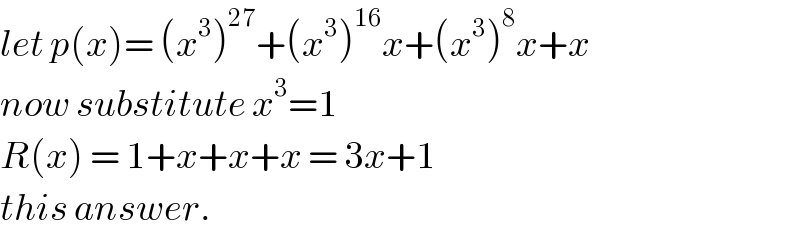
let p(x)= (x^3 )^(27) +(x^3 )^(16) x+(x^3 )^8 x+x now substitute x^3 =1 R(x) = 1+x+x+x = 3x+1 this answer.
$${let}\:{p}\left({x}\right)=\:\left({x}^{\mathrm{3}} \right)^{\mathrm{27}} +\left({x}^{\mathrm{3}} \right)^{\mathrm{16}} {x}+\left({x}^{\mathrm{3}} \right)^{\mathrm{8}} {x}+{x} \\ $$$${now}\:{substitute}\:{x}^{\mathrm{3}} =\mathrm{1} \\ $$$${R}\left({x}\right)\:=\:\mathrm{1}+{x}+{x}+{x}\:=\:\mathrm{3}{x}+\mathrm{1} \\ $$$${this}\:{answer}.\: \\ $$
Commented by mind is power last updated on 09/Jan/20
isee now ididnt see this methode befor lets proves this if P(x)=x^n , Q(x)=x^m +t n≥m let R remainder P over Q first n=m.a+r ∃!(a,r) euclidienns division x^(ma+r) =x^r (x^m )^a ,x^m =Q(x)−t x^r .(x^m )^a =x^r (Q(x)−t)^a by newtoon Methode (Q(x)−t)^a =Σ_(k=0) ^n Q(X)^k (−t)^(a−k) =(−t)^a +Σ_(k=1) ^n (Q(x))^k (−t)^(a−k) ,∀k≥1 Q(x)∣Q(x)^k (−t)^(a−k) ⇒ (Q(x)−t))^a =(−t)^a +Q(x).S(x) ⇒x^r .(x^m )^a =X^r ((−t)^a +QS(x)) =(−t)^a X^r +X^r S(X).Q(X) reminder is (−t)^a X^r How to use it reminder X^(1000) ,by X^7 +12 1000=n,m=7,t=12 1000=7.142+6,a=142,r=6 R(x)=(−12)^(142) .X^6 if P(x)=Σ_(k=0) ^n a_k X^k ,use sam idee for every K and sum the answer
$$\mathrm{isee}\: \\ $$$$\mathrm{now}\:\mathrm{ididnt}\:\mathrm{see}\:\mathrm{this}\:\mathrm{methode}\:\mathrm{befor} \\ $$$$\mathrm{lets}\:\mathrm{proves}\:\mathrm{this} \\ $$$$\mathrm{if}\:\mathrm{P}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{n}} ,\:\:\:\mathrm{Q}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{m}} +\mathrm{t} \\ $$$$\mathrm{n}\geqslant\mathrm{m}\:\:\mathrm{let}\:\mathrm{R}\:\mathrm{remainder}\:\:\mathrm{P}\:\mathrm{over}\:\mathrm{Q} \\ $$$$\mathrm{first}\:\mathrm{n}=\mathrm{m}.\mathrm{a}+\mathrm{r}\:\:\exists!\left(\mathrm{a},\mathrm{r}\right)\:\mathrm{euclidienns}\:\mathrm{division} \\ $$$$\mathrm{x}^{\mathrm{ma}+\mathrm{r}} =\mathrm{x}^{\mathrm{r}} \left(\mathrm{x}^{\mathrm{m}} \right)^{\mathrm{a}} ,\mathrm{x}^{\mathrm{m}} =\mathrm{Q}\left(\mathrm{x}\right)−\mathrm{t} \\ $$$$\mathrm{x}^{\mathrm{r}} .\left(\mathrm{x}^{\mathrm{m}} \right)^{\mathrm{a}} =\mathrm{x}^{\mathrm{r}} \left(\mathrm{Q}\left(\mathrm{x}\right)−\mathrm{t}\right)^{\mathrm{a}} \\ $$$$\mathrm{by}\:\mathrm{newtoon}\:\mathrm{Methode} \\ $$$$\left(\mathrm{Q}\left(\mathrm{x}\right)−\mathrm{t}\right)^{\mathrm{a}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{Q}\left(\mathrm{X}\right)^{\mathrm{k}} \left(−\mathrm{t}\right)^{\mathrm{a}−\mathrm{k}} =\left(−\mathrm{t}\right)^{\mathrm{a}} +\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{Q}\left(\mathrm{x}\right)\right)^{\mathrm{k}} \left(−\mathrm{t}\right)^{\mathrm{a}−\mathrm{k}} \\ $$$$,\forall\mathrm{k}\geqslant\mathrm{1}\:\:\mathrm{Q}\left(\mathrm{x}\right)\mid\mathrm{Q}\left(\mathrm{x}\right)^{\mathrm{k}} \left(−\mathrm{t}\right)^{\mathrm{a}−\mathrm{k}} \Rightarrow \\ $$$$\left.\left(\mathrm{Q}\left(\mathrm{x}\right)−\mathrm{t}\right)\right)^{\mathrm{a}} =\left(−\mathrm{t}\right)^{\mathrm{a}} +\mathrm{Q}\left(\mathrm{x}\right).\mathrm{S}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{r}} .\left(\mathrm{x}^{\mathrm{m}} \right)^{\mathrm{a}} =\mathrm{X}^{\mathrm{r}} \left(\left(−\mathrm{t}\right)^{\mathrm{a}} +\mathrm{QS}\left(\mathrm{x}\right)\right) \\ $$$$=\left(−\mathrm{t}\right)^{\mathrm{a}} \mathrm{X}^{\mathrm{r}} +\mathrm{X}^{\mathrm{r}} \mathrm{S}\left(\mathrm{X}\right).\mathrm{Q}\left(\mathrm{X}\right)\:\:\mathrm{reminder}\:\mathrm{is}\:\:\:\left(−\mathrm{t}\right)^{\mathrm{a}} \mathrm{X}^{\mathrm{r}} \\ $$$$\mathrm{How}\:\mathrm{to}\:\mathrm{use}\:\mathrm{it}\: \\ $$$$\mathrm{reminder}\:\mathrm{X}^{\mathrm{1000}} ,\mathrm{by}\:\mathrm{X}^{\mathrm{7}} +\mathrm{12} \\ $$$$\mathrm{1000}=\mathrm{n},\mathrm{m}=\mathrm{7},\mathrm{t}=\mathrm{12} \\ $$$$\mathrm{1000}=\mathrm{7}.\mathrm{142}+\mathrm{6},\mathrm{a}=\mathrm{142},\mathrm{r}=\mathrm{6} \\ $$$$\mathrm{R}\left(\mathrm{x}\right)=\left(−\mathrm{12}\right)^{\mathrm{142}} .\mathrm{X}^{\mathrm{6}} \\ $$$$\mathrm{if}\:\mathrm{P}\left(\mathrm{x}\right)=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{k}} \mathrm{X}^{\mathrm{k}} ,\mathrm{use}\:\mathrm{sam}\:\mathrm{idee}\:\mathrm{for}\:\mathrm{every}\:\mathrm{K}\:\mathrm{and}\:\mathrm{sum}\:\mathrm{the}\:\mathrm{answer} \\ $$$$ \\ $$
Commented by john santu last updated on 09/Jan/20
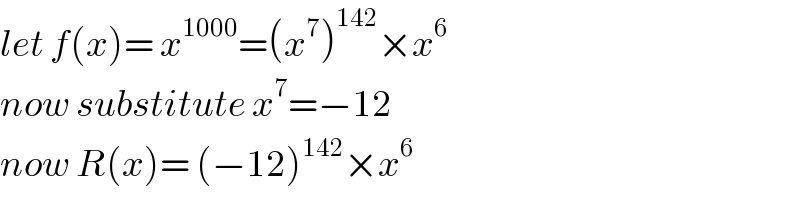
let f(x)= x^(1000) =(x^7 )^(142) ×x^6 now substitute x^7 =−12 now R(x)= (−12)^(142) ×x^6
$${let}\:{f}\left({x}\right)=\:{x}^{\mathrm{1000}} =\left({x}^{\mathrm{7}} \right)^{\mathrm{142}} ×{x}^{\mathrm{6}} \\ $$$${now}\:{substitute}\:{x}^{\mathrm{7}} =−\mathrm{12} \\ $$$${now}\:{R}\left({x}\right)=\:\left(−\mathrm{12}\right)^{\mathrm{142}} ×{x}^{\mathrm{6}} \\ $$
Commented by TawaTawa last updated on 09/Jan/20
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *